
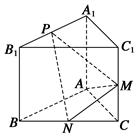
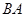 为
为 轴,
轴,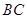 为
为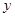 轴,
轴,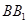 为
为 轴建立空间直角坐标系
轴建立空间直角坐标系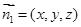 为平面
为平面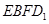 的法向量,又正方体的棱长为1,
的法向量,又正方体的棱长为1,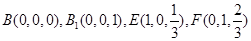
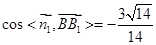 ,得到结论
,得到结论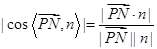 =
=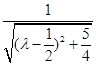 (*)
(*)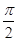 ],当θ最大时,sin θ最大,tan θ最大(θ=
],当θ最大时,sin θ最大,tan θ最大(θ=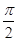 除外),
除外),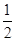 时,(sin θ)max=
时,(sin θ)max=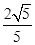 ,(tan θ)max=2
,(tan θ)max=2 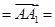 (0,0,1).设平面PMN的一个法向量为m=(x,y,z),
(0,0,1).设平面PMN的一个法向量为m=(x,y,z),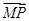 =(λ,-1,
=(λ,-1,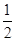 ).
).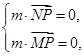 求出法向量,然后结合二面角得到解得λ=-
求出法向量,然后结合二面角得到解得λ=-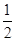 .
.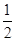 ,
,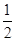 ,0),
,0),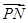 =(
=(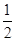 -λ,
-λ, 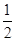 ,-1),
,-1),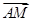 =(0,1,
=(0,1, 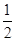 ).
).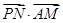 =(
=(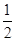 -λ)×0+
-λ)×0+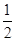 ×1-1×
×1-1×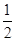 =0,
=0, 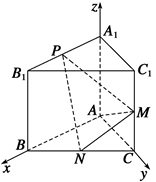
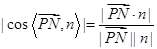 =
=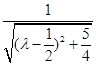 (*)
(*)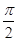 ],当θ最大时,sin θ最大,tan θ最大(θ=
],当θ最大时,sin θ最大,tan θ最大(θ=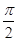 除外),
除外),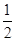 时,(sin θ)max=
时,(sin θ)max=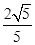 ,(tan θ)max=2 -----------6分
,(tan θ)max=2 -----------6分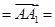 (0,0,1).设平面PMN的一个法向量为m=(x,y,z),
(0,0,1).设平面PMN的一个法向量为m=(x,y,z),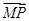 =(λ,-1,
=(λ,-1,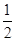 ).
).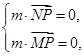
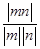 =
=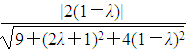 =
=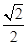 ,解得λ=-
,解得λ=-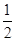 .
.

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com