
【题目】己知长方形![]() ,
,![]() 为坐标原点,
为坐标原点,![]() 点坐标为
点坐标为![]() ,
,![]() 点在
点在![]() 轴的正半轴上,
轴的正半轴上,![]() 点在
点在![]() 轴的正半轴上,
轴的正半轴上,![]() 是线段
是线段![]() 上的动点,设
上的动点,设![]() ,已知点
,已知点![]() 在第一象限且是直线
在第一象限且是直线![]() 上一点,若
上一点,若![]() 是等腰直角三角形.
是等腰直角三角形.
(![]() )求点
)求点![]() 的坐标并写出解题过程.
的坐标并写出解题过程.
(![]() )直角
)直角![]() 向下平移
向下平移![]() 个单位后,在该直线上是否存在点
个单位后,在该直线上是否存在点![]() ,使
,使![]() 是等腰直角三角形.
是等腰直角三角形.

【答案】(![]() )
)![]() ;(
;(![]() )存在点
)存在点![]() ,使
,使![]() 为等腰直角三角形,
为等腰直角三角形,![]() 坐标为
坐标为![]() ,
,![]() ,
,![]() .
.
【解析】试题分析:
(1)由点D和点A都在直线y=2x+6上可知,若△APD是等腰直角三角形,则只能是点A为直角顶点,如图,过点D作DE⊥y轴于点E,则易证![]() ≌
≌![]() ,由此可得
,由此可得![]() ,
,![]() ,从而可得点D的坐标为(6-m,14),将D的坐标代入y=2x+6中,解得m的值,即可得到点D的坐标;
,从而可得点D的坐标为(6-m,14),将D的坐标代入y=2x+6中,解得m的值,即可得到点D的坐标;
(2)将直线y=2x+6向下平移12个单位所得新直线的解析式为:y=2x-6,由图可知,点A、P在直线y=2x-6两侧,故当△APD为等腰直角三角形时,存在∠ADP=90°,∠APD=90°两种可能情况,其中当∠ADP=90°时,又存在点D在点A的上方和下方两种情况,如图2、图3和图4,然后结合已知条件进行推理计算即可.
试题解析:
(![]() )∵点A、D都在直线y-2x+6上,
)∵点A、D都在直线y-2x+6上,
∴当△APD是等腰直角三角形时,只能是点A为直角顶点,
如图1:过![]() 作
作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() ,
,
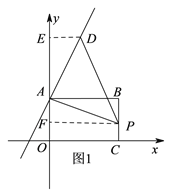
∵![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
代入![]() 中得:-2m+6=14,解得:m=2,
中得:-2m+6=14,解得:m=2,
∴![]() ;
;
(![]() )存在点
)存在点![]() ,使
,使![]() 为等腰直角三角形,
为等腰直角三角形,
直线![]() 向下平移
向下平移![]() 个单位后变成
个单位后变成![]() ,
,
当![]() 时,
时,
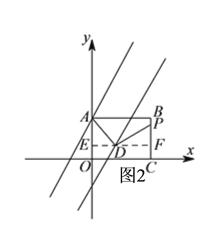
①、如图2所示,过![]() 作
作![]() 交
交![]() 、
、![]() 于
于![]() 、
、![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
设![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]()
![]() .
.
∴![]() ,
,
代入![]() 中得,
中得,
![]() ,
,
∴![]() .
.
②如图3所示:
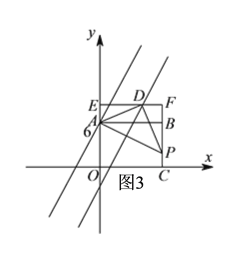
过![]() 作
作![]() 平行线
平行线![]() 交
交![]() 延长线于
延长线于![]() ,
,
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
代入![]() 中得,
中得,
![]() ,
,
∴![]() .
.
③当![]() 时,如图4,过
时,如图4,过![]() 作
作![]() ,交其垂线
,交其垂线![]() 于
于![]() ,
,
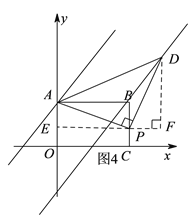
∴![]() ≌
≌![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
代入![]() 中,
中,
![]() ,
,
∴![]() ,
,
综上所述,点D的坐标为![]() ,
,![]() ,
,![]() .
.


科目:初中数学 来源: 题型:
【题目】(10分)已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.
(1)如图①,点D在线段BC上移动时,直接写出∠BAD和∠CAE的大小关系;
(2)如图②,点D在线段BC的延长线上移动时,猜想∠DCE的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
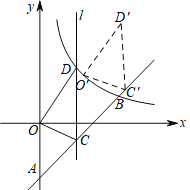
【题目】如图,一次函数y=kx-4(k≠0)的图象与y轴交于点A,与反比例函数y=![]() (x>0)的图象交于点B(6,b).
(x>0)的图象交于点B(6,b).
(1)b=__________;k=__________.
(2)点C是直线AB上的动点(与点A,B不重合),过点C且平行于y轴的直线l交这个反比例函数的图象于点D,当点C的横坐标为3时,得△OCD,现将△OCD沿射线AB方向平移一定的距离(如图),得到△O′C′D′,若点O的对应点O′落在该反比例函数图象上,求点O′,D′的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(庆阳中考)现在的青少年由于沉迷电视、手机、网络游戏等,视力日渐减退,某市为了了解学生的视力变化情况,从全市九年级随机抽取了1 500名学生,统计了每个人连续三年视力检查的结果,根据视力在4.9以下的人数变化制成折线统计图,并对视力下降的主要因素进行调查,制成扇形统计图.
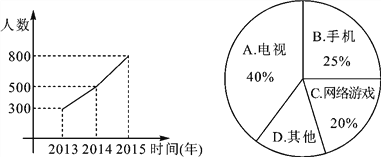
解答下列问题:
(1)图中D所在扇形的圆心角度数为______;
(2)若2016年全市共有30 000名九年级学生,请你估计视力在4.9以下的学生约有多少名?
(3)根据扇形统计图信息,你觉得中学生应该如何保护视力?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A,B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12 m,由此他就知道了A,B间的距离,有关他这次探究活动的描述错误的是( )
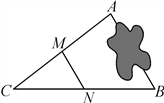
A. AB=24 m B. MN∥AB C. △CMN∽△CAB D. CM∶MA=1∶2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com