
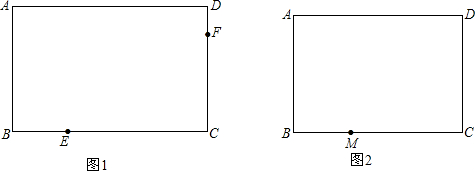
 S矩形ECDG,S△EGH=
S矩形ECDG,S△EGH= S矩形ABEG,
S矩形ABEG, S四边形ABCD;
S四边形ABCD;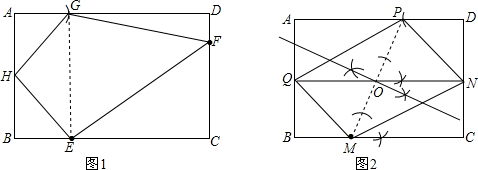
 (BM+AP)=
(BM+AP)= AD,NO=
AD,NO= (MC+DP)=
(MC+DP)= BC,
BC, S矩形AQND,S△EQMN=
S矩形AQND,S△EQMN= S矩形BCNQ,
S矩形BCNQ, S四边形ABCD.
S四边形ABCD.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 5、如图,东梅中学要在教学楼后面的空地上用40米长的竹篱笆围出一个矩形地块作生物园,矩形的一边用教学楼的外墙,其余三边用竹篱笆.设矩形的宽为x,面积为y.
5、如图,东梅中学要在教学楼后面的空地上用40米长的竹篱笆围出一个矩形地块作生物园,矩形的一边用教学楼的外墙,其余三边用竹篱笆.设矩形的宽为x,面积为y.查看答案和解析>>
科目:初中数学 来源: 题型:
 19、如图,东梅中学要在教学楼后面的空地上用30米长的竹篱笆围出一个矩形地块作生物园,矩形的一边用教学楼的外墙,其余三边用竹篱笆.设矩形的一边为x,面积为y.
19、如图,东梅中学要在教学楼后面的空地上用30米长的竹篱笆围出一个矩形地块作生物园,矩形的一边用教学楼的外墙,其余三边用竹篱笆.设矩形的一边为x,面积为y.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,东梅中学要在教学楼后面的空地上用20米长的竹篱笆围出一个矩形地块作生物园,矩形的一边用教学楼的外墙,其余三边用竹篱笆.怎样围成一个面积为50m2的矩形地块生物园?
如图,东梅中学要在教学楼后面的空地上用20米长的竹篱笆围出一个矩形地块作生物园,矩形的一边用教学楼的外墙,其余三边用竹篱笆.怎样围成一个面积为50m2的矩形地块生物园?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com