
| 1 |
| 2 |
| 1 |
| 2 |
|


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
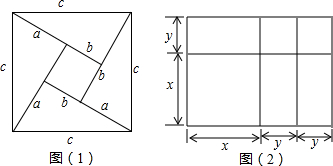
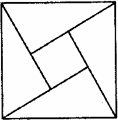
 如图是2002年8月在北京召开的国际数学家大会的会标,它取材于我国古代数学家赵爽的《勾股圆方图》,由四个全等的直角三角形和一个小正方形的拼成的大正方形,如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短边为a,较长边为b,那么(a+b)2的值是
如图是2002年8月在北京召开的国际数学家大会的会标,它取材于我国古代数学家赵爽的《勾股圆方图》,由四个全等的直角三角形和一个小正方形的拼成的大正方形,如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短边为a,较长边为b,那么(a+b)2的值是查看答案和解析>>
科目:初中数学 来源:测试专家八年级数学下册 第18章 勾股定理、综合检测题 题型:013
如图所示,我国古代数学家赵爽的《勾股圆方图》是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形,如果大正方形的面积是13,小正方形的面积是1,直角三角形较短的直角边为a,较长的直角边为b,那么![]() 的值为
的值为
A.13
B.19
C.25
D.169
查看答案和解析>>
科目:初中数学 来源:期末题 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:
如图1是2002年8月在北京召开的国际数学家大会的会标,它取材于我国古代数学家赵爽的《勾股圆方图》,由四个全等的直角三角形和一个小正方形的拼成的大正方形.
(1)如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短边为a,较长边为b,
那么(![]() +
+![]() )2的值是 ;
)2的值是 ;
(2)若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是 .
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com