
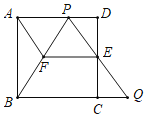
【题目】如图,在边长为l的正方形ABCD中,E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.
(1)求证:![]() ;
;
(2)过点E作![]() 交PB于点F,连结AF,当
交PB于点F,连结AF,当![]() 时,①求证:四边形AFEP是平行四边形;
时,①求证:四边形AFEP是平行四边形;
②请判断四边形AFEP是否为菱形,并说明理由.
【答案】(1)见解析;(2)①见解析;②当![]() 时,四边形AFEP是菱形
时,四边形AFEP是菱形
【解析】
(1)由四边形ABCD是正方形知![]() ,由E是CD的中点知
,由E是CD的中点知![]() ,结合
,结合![]() 即可得证;
即可得证;
(2)①由![]() 知
知![]() ,结合
,结合![]() 得
得![]() ,由
,由![]() 知
知![]() ,再由
,再由![]() 知
知![]() ,根据
,根据![]() 中
中![]() 知
知![]() ,从而得
,从而得![]() ,据此即可证得
,据此即可证得![]() ,从而得证;
,从而得证;
②设![]() ,则
,则![]() ,若四边形AFEP是菱形,则
,若四边形AFEP是菱形,则![]() ,由
,由![]() 得关于x的方程,解之求得x的值,从而得出四边形AFEP为菱形的情况.
得关于x的方程,解之求得x的值,从而得出四边形AFEP为菱形的情况.
解:(1)![]() 四边形ABCD是正方形,
四边形ABCD是正方形,
![]() ,
,
![]() E是CD的中点,
E是CD的中点,
![]() ,
,
又![]() ,
,
![]() ;
;
(2)①![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四边形AFEP是平行四边形;
四边形AFEP是平行四边形;
②当![]() 时,四边形AFEP是菱形.
时,四边形AFEP是菱形.
设![]() ,则
,则![]() ,
,
若四边形AFEP是菱形,则![]() ,
,
![]() ,E是CD中点,
,E是CD中点,
![]() ,
,
在![]() 中,由
中,由![]() 得
得![]() ,
,
解得![]() ,
,
即当![]() 时,四边形AFEP是菱形.
时,四边形AFEP是菱形.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】点A的坐标是A(x,y),从1、2、3这三个数中任取一个数作为x的值,再从余下的两个数中任取一个数作为y的值.则点A落在直线y=﹣x+5与直线y=![]() x及y轴所围成的封闭区域内(含边界)的概率是_____.
x及y轴所围成的封闭区域内(含边界)的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在菱形![]() 中
中![]() ,
,![]() ,边
,边![]() 上一动点
上一动点![]() 从点
从点![]() 出发向点
出发向点![]() 匀速运动,速度为
匀速运动,速度为![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,以
,以![]() 为边长作等边
为边长作等边![]() ,点
,点![]() ,
,![]() 在直线
在直线![]() 的异侧,连接
的异侧,连接![]() .点
.点![]() 的运动时间为
的运动时间为![]() .
.
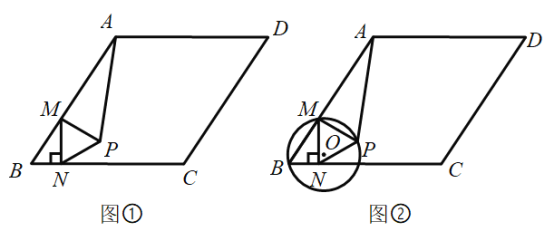
(1)当![]() 时,
时,![]() _______
_______![]() ;(直接写出答案)
;(直接写出答案)
(2)连接![]() ,若
,若![]() 为等腰三角形,求
为等腰三角形,求![]() 的值;
的值;
(3)如图②,经过点![]() 、
、![]() 、
、![]() 作
作![]() ,连接
,连接![]() ,当
,当![]() 与
与![]() 相切时,则
相切时,则![]() 的值等于_______
的值等于_______![]() (直接写出答案)
(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1.已知⊙M与x轴交于A、B两点,与y轴交于C、D两点,A、B两点的横坐标分别为﹣1和7,弦AB的弦心距MN为3,
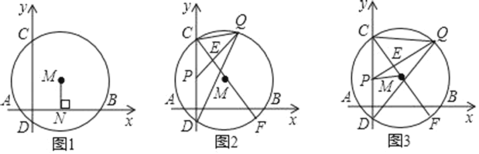
(1)求⊙M的半径;
(2)如图2,P在弦CD上,且CP=2,Q是弧BC上一动点,PQ交直径CF于点E,当∠CPQ=∠CQD时,
①判断线段PQ与直径CF的位置关系,并说明理由;
②求CQ的长;
(3)如图3.若P点是弦CD上一动点,Q是弧BC上一动点,PQ交直径CF于点E,当∠CPQ与∠CQD互余时,求△PEM面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备为“中国古诗词”朗诵比赛购买奖品.已知在中央商场购买3个甲种奖品和2个乙种奖品共需120元;购买5个甲种奖品和4个乙种奖品共需210元.
(1)求甲、乙两种奖品的单价;
(2)学校计划购买甲、乙两种奖品共80个,且此次购买奖品的费用不超过1500元.正逢中央商场促销,所有商品一律八折销售,求学校在中央商场最多能购买多少个甲种奖品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯经营店销售![]() ,
,![]() 两种品牌儿童手机,今年进货和销售价格如下表:
两种品牌儿童手机,今年进货和销售价格如下表:
|
| |
进货价格(元/只) | 1000 | 1100 |
销售价格(元/只) |
| 1500 |
已知![]() 型手机去年4月份销售总额为3.6万元,今年经过改造升级后每部销售价比去年增加400元.今年4月份
型手机去年4月份销售总额为3.6万元,今年经过改造升级后每部销售价比去年增加400元.今年4月份![]() 型手机的销售数量与去年4月份相同,而销售总额为5.4万元.
型手机的销售数量与去年4月份相同,而销售总额为5.4万元.
(1)求今年4月份![]() 型手机的销售价是多少元?
型手机的销售价是多少元?
(2)该店计划6月份再进一批![]() 型和
型和![]() 型手机共50部且
型手机共50部且![]() 型手机数量不超过
型手机数量不超过![]() 型手机数量的2倍,应如何进货才能使这批儿童手机获利最多?
型手机数量的2倍,应如何进货才能使这批儿童手机获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,菱形![]() 在第一象限内,边
在第一象限内,边![]() 与
与![]() 轴平行,
轴平行,![]() ,
,![]() 两点的纵坐标分别为
两点的纵坐标分别为![]() ,
,![]() ,反比例函数
,反比例函数![]() 的图象经过
的图象经过![]() ,
,![]() 两点,菱形
两点,菱形![]() 的面积为
的面积为![]() ,则
,则![]() 的值为________.
的值为________.
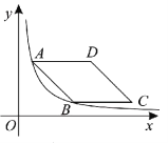
查看答案和解析>>
科目:初中数学 来源: 题型:
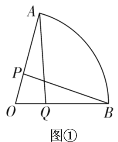
【题目】在扇形![]() 中,
中,![]() ,半径
,半径![]() ,点P为
,点P为![]() 上任一点(不与A、O重合).
上任一点(不与A、O重合).
(1)如图①,Q是![]() 上一点,若
上一点,若![]() ,求证:
,求证:![]() .
.
(2)如图②,将扇形沿![]() 折叠,得到O的对称点
折叠,得到O的对称点![]() .
.
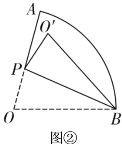
①若点![]() 落在
落在![]() 上,求
上,求![]() 的长;
的长;
②当![]() 与扇形
与扇形![]() 所在的圆相切时,求折痕的长.(注:本题结果不取近似值)
所在的圆相切时,求折痕的长.(注:本题结果不取近似值)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com