
【题目】定义:有一组邻边均和一条对角线相等的四边形叫做邻和四边形.
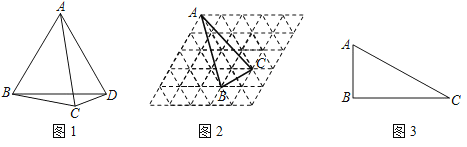
(1)如图1,四边形ABCD中,∠ABC=70°,∠BAC=40°,∠ACD=∠ADC=80°,求证:四边形ABCD是邻和四边形.
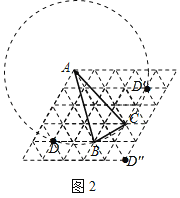
(2)如图2,是由50个小正三角形组成的网格,每个小正三角形的顶点称为格点,已知A,B,C三点的位置如图,请在网格图中标出所有的格点D,使得以A,B,C,D为顶点的四边形为邻和四边形.
(3)如图3,△ABC中,∠ABC=90°,AB=4,BC=4![]() ,若存在一点D,使四边形ABCD是邻和四边形,求邻和四边形ABCD的面积.
,若存在一点D,使四边形ABCD是邻和四边形,求邻和四边形ABCD的面积.
【答案】(1)详见解析;(2)详见解析;(3)24![]() 或16
或16![]() .
.
【解析】
(1)根据题意先由三角形的内角和为180°求得∠ACB的度数,从而根据等腰三角形的判定证得AB=AC=AD,按照邻和四边形的定义即可得出结论;
(2)根据题意以点A为圆心,AB长为半径画圆,与网格的交点,以及△ABC外侧与点B和点C组成等边三角形的网格点即为所求;
(3)由题意先根据勾股定理求得AC的长,再分类计算即可:①当DA=DC=AC时;②当CD=CB=BD时;③当DA=DC=DB或AB=AD=BD时.
解:(1)∵∠ACB=180°﹣∠ABC﹣∠BAC=70°,
∴∠ACB=∠ABC,
∴AB=AC.
∵∠ACD=∠ADC,
∴AC=AD,
∴AB=AC=AD.
∴四边形ABCD是邻和四边形.
(2)如图,格点D,D',D'即为所求作的点.
(3)∵在△ABC中,∠ABC=90°,AB=4,BC=4![]() ,
,
∴AC=![]() =8,
=8,
显然AB,BC,AC互不相等.分两种情况讨论:
①当DA=DC=AC时,如图所示:
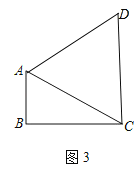
∴S△ADC=![]() AC2=16
AC2=16![]() ,S△ABC=
,S△ABC=![]() AB×BC=8
AB×BC=8![]() .
.
∴S四边形ABCD=S△ADC+S△ABC=24![]() ;
;
②当CD=CB=BD时,如图所示:
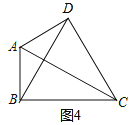
∴S△BDC=![]() BC2=12
BC2=12![]() ,S△ADB=
,S△ADB=![]() AB(
AB(![]() BC)=4
BC)=4![]() ,
,
∴S四边形ABCD=S△BDC+S△ADB=16![]() ;
;
③当DA=DC=DB或AB=AD=BD时,邻和四边形ABCD不存在.
∴邻和四边形ABCD的面积是24![]() 或16
或16![]() .
.


科目:初中数学 来源: 题型:
【题目】某电器商场销售A,B两种型号计算器,两种计算器的进货价格分别为每台30元,40元. 商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利120元.
(1)求商场销售A,B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
(2)商场准备用不多于2500元的资金购进A,B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
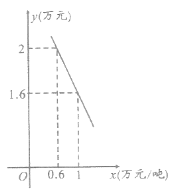
【题目】某蔬菜批发公司用实际行动支持抗击新冠肺炎疫情,为确保市民在疫情期间的蔬菜供应,以平均每吨![]() 万元的价格购进一批蔬菜,已知这批蔬菜通过网络在市场上的日销售量
万元的价格购进一批蔬菜,已知这批蔬菜通过网络在市场上的日销售量![]() (吨)与销售价格
(吨)与销售价格![]() (万元/吨)之间的函数关系如下图所示.
(万元/吨)之间的函数关系如下图所示.
(1)求日销售量![]() 与销售价格
与销售价格![]() 之间的函数关系式; (不要求写
之间的函数关系式; (不要求写![]() 的取值范围)
的取值范围)
(2)如果要确保日销售量不小于![]() 吨,求最大毛利润.(假设:毛利润=销售额-购进成本)
吨,求最大毛利润.(假设:毛利润=销售额-购进成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了响应国家提出的“每天锻炼1小时”的号召,某校积极开展了形式多样的“阳光体育”运动,毛毛对该班同学参加锻炼的情况进行了统计(每人只能选其中一项),并绘制了如图两个统计图,请根据图中提供的信息解答下列问题:
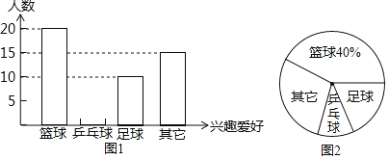
(1)毛毛这次一共调查了多少名学生?
(2)补全条形统计图,并求出扇形统计图中“足球”所在扇形的圆心角度数;
(3)若该校有1800名学生,请估计该校喜欢乒乓球的学生约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
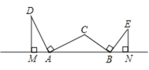
【题目】如图,在△ABC 中,∠ACB 为钝角,边 AC 绕点 A 沿逆时针方向旋转 90°得到AD,边 BC 绕点 B 沿顺时针方向旋转 90°得到 BE,作 DM⊥AB 于点 M,EN⊥AB于 点 N, 若 AB=10,EN=4, 则 DM=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
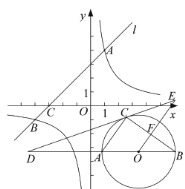
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与反比例函数
,与反比例函数![]() 的图象交于点
的图象交于点![]() 和点
和点![]() .
.
(1)求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)若点![]() 是
是![]() 轴上一点,且
轴上一点,且![]() ,直接写出点
,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
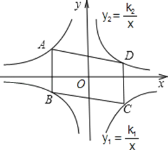
【题目】如图,平行四边形ABCD的顶点为A、C在双曲线y1=![]() 上,B、D在双曲线
上,B、D在双曲线![]() 上,k1=2k2(k1>0),AB∥y轴,
上,k1=2k2(k1>0),AB∥y轴,![]() =24,则k2的值为( )
=24,则k2的值为( )
A.4B.-4C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,点O在斜边AB上,以O为圆心,OB长为半径作⊙O,与BC交于点D,连结AD,已知
,点O在斜边AB上,以O为圆心,OB长为半径作⊙O,与BC交于点D,连结AD,已知![]() .
.
(1)求证:AD是⊙O的切线;
(2)若BC=8,![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
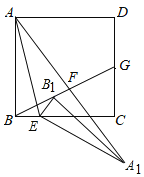
【题目】如图,在正方形ABCD中,点E是BC边上一点,连接AE,将△ABE绕点E顺时针旋转得到△A1B1E,点B1在正方形ABCD内,连接AA1、BB1;
(1)求证:△AA1E∽△BB1E;
(2)延长BB1分别交线段AA1,DC于点F、G,求证:AF=A1F;
(3)在(2)的条件下,若AB=4,BE=1,G是DC的中点,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com