
����Ŀ��ijУ������1����50��ѧ����Ҫ�μ���������ѡһ����ѡ��Ŀ���ԣ�����ѧ��������ѡ��Ŀ�����ͳ�Ʊ����£�
��ѡ��Ŀ | ���� | Ƶ�� |
������Զ | 9 | 0.18 |
�������� | 12 | a |
һ�������� | 8 | 0.16 |
Ͷ��ʵ���� | b | 0.32 |
��Ǧ�� | 5 | 0.10 |
�ϼ� | 50 | 1 |
��1����a��b��ֵ��
��2����������ѡ��Ŀ��������ռ�������Ƴ�����ͳ��ͼ����һ������������Ӧ���ε�Բ�ĽǵĶ�����
��3����ѡ������Ǧ��ѧ���У���3��������2��Ů����Ϊ���˽�ѧ����ѵ��Ч��������5��ѧ���������ȡ����ѧ��������Ǧ����ԣ�������ȡ������ѧ����������һ��Ů���ĸ��ʣ�
���𰸡���1��a=0.24��b=16����2����ͼ�������� 57.6�㣻��3����ȡ������ѧ����������һ��Ů���ĸ���Ϊ![]() ��
��
�������������������1���ɱ������a��b��ֵ���ɣ�
��2���ɱ�ʾ��������ͳ��ͼ���������������Ӧ���ε�Բ�ĽǵĶ������ɣ�
��3���б��ó����еȿ��ܵ���������ҳ���ȡ������ѧ����ǡ��һ��Ů����������������������ʣ�
�����������1��������ã�a=1����0.18+0.16+0.32+0.10��=0.24��b=![]() ��0.32=16��
��0.32=16��
��2����������ͳ��ͼ����ͼ��ʾ��

������ã�360���0.10=36����
��3���������ΪA��B��C��Ů�����ΪD��E����ö�ٷ��ɵã�AB��AC��AD��AE��BC��BD��BE��CD��CE��DE��10�֣�����DEΪŮŮ��ϣ�AB��AC��BC��������ϣ�����ȡ������ѧ��������ѧ����ǡ��һ��Ů���ĸ���Ϊ��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����Ա��ij��ҵ����һ�ָ���ҵ�����������Ʒ������ҵҪ40����������Աÿ���ɻ���40Ԫ������Ա���ڲ�������ǰ���£�Ϊ����������������ҵΪ�˽��������ɱ�����Э�̴��Э�飬�����ҵ����40������ʱ��ÿ��Ҫ1������ÿ������1Ԫ��
��1����ÿ������![]() ��Ԫ��ʱ������Ա����Ϊ
��Ԫ��ʱ������Ա����Ϊ![]() ��Ԫ������д��
��Ԫ������д��![]() ����
����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��2����ÿ������20Ԫʱ���ʴ�ʱ��ҵ�蹺����Ʒ���ټ�����ʱ����Ա�������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��![]() ��ͬһ��ֱ���ϣ�
��ͬһ��ֱ���ϣ�![]() ƽ��
ƽ��![]() .
.
��1����գ���![]() ����Ľ��� ��
����Ľ��� ��
��2����![]() ����
����![]() �Ķ�����
�Ķ�����
��3����֤��![]() ��
��![]() ��ƽ����.
��ƽ����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() ��
��![]() ��
��![]() ���㣬�������¶��壺������һ����������������ľ���ǡ������2����������ϵ����Ƹõ������������������������.���������ϵ�
���㣬�������¶��壺������һ����������������ľ���ǡ������2����������ϵ����Ƹõ������������������������.���������ϵ�![]() ��
��![]() ��
��![]() ����ʾ�����ֱ�Ϊ1, 3��4����ʱ��
����ʾ�����ֱ�Ϊ1, 3��4����ʱ��![]() �ǵ�
�ǵ�![]() ��
��![]() ������������.
������������.
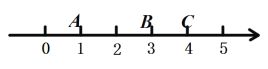
��1������![]() ��ʾ��-2����
��ʾ��-2����![]() ��ʾ��1�����и���-1, 2, 4, 6����Ӧ�ĵ�ֱ���
��ʾ��1�����и���-1, 2, 4, 6����Ӧ�ĵ�ֱ���![]() ,
,![]() ��
��![]() ��
��![]() �������ǵ�
�������ǵ�![]() ��
��![]() ����������������
����������������
��2����![]() ��ʾ��-10����
��ʾ��-10����![]() ��ʾ��15��
��ʾ��15��![]() Ϊ������һ�����㣺
Ϊ������һ�����㣺
������![]() �ڵ�
�ڵ�![]() ����࣬�ҵ�
����࣬�ҵ�![]() �ǵ�
�ǵ�![]() ��
��![]() �����������������ʱ��
�����������������ʱ��![]() ��ʾ������
��ʾ������
������![]() �ڵ�
�ڵ�![]() ���Ҳ࣬��
���Ҳ࣬��![]() ��
��![]() ��
��![]() �У���һ����ǡ�����������������������������ֱ��д����ʱ��
�У���һ����ǡ�����������������������������ֱ��д����ʱ��![]() ��ʾ����.
��ʾ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��֪������ABCD��AB=8cm��BC=10cm���ڱ�CD��ȡһ��E������ADE�۵�ʹ��Dǡ������BC���ϵĵ�F����CE�ij�Ϊ___________.
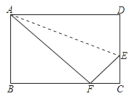
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�E��F�ֱ�ΪBC��AD���е㣬AE��CF�ֱ�BD�ڵ�M��N�����ı��� AMCN����ABCD�������Ϊ�� ��
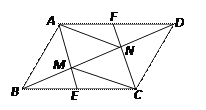
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
���𰸡�B
������������������ƽ���ı���һ����ͶԱ��е������һ�����ȷ�ƽ���ı��ε�һ�Խ��ߣ��ɵã�![]() ���ɵó�����.
���ɵó�����.
��⣺������ɵã�M��NΪ�߶�BD�����ȷֵ㣬
��![]()
![]()
��ѡB.
�㾦��ƽ���ı���һ����ͶԱ��е������һ�����ȷ�ƽ���ı��ε�һ�Խ���.
�����͡���ѡ��
��������
10
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�A(2��0)��B(0��2)����M���߶�AB�ϣ���MO+MP��Сֵ��ƽ��Ϊs������P��x������ӵ�O�˶�����Aʱ(���P�ĺ�����Ϊx)��s����x�ĺ���ͼ�����Ϊ�� ��
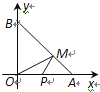
A.  B.
B. 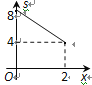 C.
C. 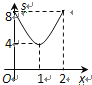 D.
D. 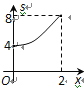
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�и�������Ϣ������������⣺
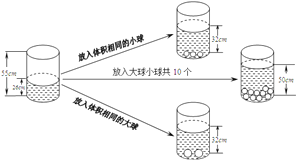
��1������һ��С��ˮ������ ��![]() ������һ������ˮ������
������һ������ˮ������ ![]() ��
��
��2�����Ҫʹˮ��������50![]() ��Ӧ�������С������ٸ���
��Ӧ�������С������ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC����C=90����AC=12��BC=6��һ���߶�PQ=AB��P��Q����ֱ���AC����A�Ҵ�ֱ��AC������AX���˶���Ҫʹ��ABC����QPAȫ�ȣ���AP= ______ ��
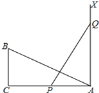
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������x��һԪ���η���![]() ������ʵ������������һ����Ϊ��һ������2������������ķ���Ϊ�����������������¹��ڱ������̵�˵������ȷ����________����д��������ȷ˵������ţ���
������ʵ������������һ����Ϊ��һ������2������������ķ���Ϊ�����������������¹��ڱ������̵�˵������ȷ����________����д��������ȷ˵������ţ���
������![]() �DZ������̣�
�DZ������̣�
����![]() �DZ������̣���
�DZ������̣���![]() ��
��
������![]() �ڷ���������
�ڷ���������![]() ��ͼ���ϣ������
��ͼ���ϣ������![]() �ķ���
�ķ���![]() �DZ������̣�
�DZ������̣�
��������![]() �DZ������̣�����������
�DZ������̣�����������![]() ��
�� ![]() ����������
����������![]() �ϣ���
�ϣ���![]() ��һ����Ϊ
��һ����Ϊ![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com