
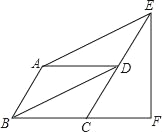
【题目】如图,平行四边形ABCD中,∠ABC=60°,点E、F分别在CD、BC的延长线上,AE∥BD,EF⊥BF,垂足为点F,DF=2.
(1)求证:D是EC中点;
(2)求EF的长.
【答案】(1)证明见解析;(2)2![]() .
.
【解析】
(1)根据平行四边形的对边平行可以得到AB∥CD,又AE∥BD,可以证明四边形ABDE是平行四边形,所以AB=DE,故D是EC的中点;
(2)连接DF,则△EFC是直角三角形,根据直角三角形斜边上的中线等于斜边的一半可以得到△CDF是等边三角形,根据勾股定理即可得到结论.
(1)证明:在平行四边形ABCD中,
AB∥CD,且AB=CD,
又∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=DE,
∴CD=DE,
即D是EC的中点;
(2)解:∵EF⊥BF,
∴△EFC是直角三角形
又∵D是EC的中点,
∴DF=CD=DE=2,
∵AB∥CD,∠ABC=60°,
∴∠DCF=60°,
∴△DCF是等边三角形,
∴CF=2,
∴在Rt△ECF中
EF=![]() =
=![]() =2
=2![]() .
.
故答案为:(1)证明见解析;(2)2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: + =( +
,填空: + =( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
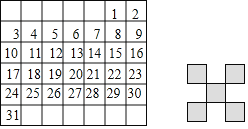
【题目】如图是某月的月历,用如图恰好能完全遮盖住月历表中的五个数字,设带阴影的“![]() ”形中的5个数字的最小数为a.
”形中的5个数字的最小数为a.
![]() 请用含a的代数式表示这5个数;
请用含a的代数式表示这5个数;
![]() 这五个数的和与“
这五个数的和与“![]() ”形中心的数有什么关系?
”形中心的数有什么关系?
![]() 盖住的5个数字的和能为105吗?为什么?
盖住的5个数字的和能为105吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技馆门票价格规定如下表:
购票张数 |
|
| 100张以上 |
每张票的价格 | 18元 | 15元 | 10元 |
风鸣学校七年级![]() 、
、![]() 两个科技班共103人去科技馆,其中
两个科技班共103人去科技馆,其中![]() 班有40多人不足50人
班有40多人不足50人![]() 经计算,如果两个班都以班为单位购票,则一共应付1686元.
经计算,如果两个班都以班为单位购票,则一共应付1686元.
![]() 如果两个班联合起来,作为一个团体购票,可以省______元
如果两个班联合起来,作为一个团体购票,可以省______元![]()
![]() 七年级
七年级![]() 班有多少学生?
班有多少学生?
![]() 如果七年级
如果七年级![]() 班单独组织去科技馆,作为组织者,你如何购票才最省钱?
班单独组织去科技馆,作为组织者,你如何购票才最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把2张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m,宽为n)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示.阴影部分刚好能分割成两张形状大小不同的小长方形卡片(如图③),则分割后的两个阴影长方形的周长和是( )
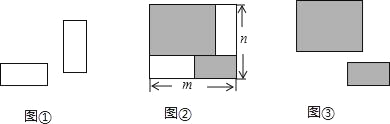
A. 4mB. 2(m+n)C. 4nD. 4(m﹣n)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )

A. 2个 B. 3个 C. 4个 D. 无数个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OM,ON分别是∠BOC和∠AOC的角平分线,∠AOB=86°,(1)∠MON=______(度);(2)当OC在∠AOB内绕点O转动时,∠MON的值______改变(填“会”或“不会”).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com