
【题目】已知二次函数![]() 的顶点坐标为
的顶点坐标为![]() ,
,![]() .
.
(1)若该函数图象过点![]() .
.
①求该函数解析式;
②![]() ,函数图象上点
,函数图象上点![]() 到x轴的距离最小值为1,则t的值为______;
到x轴的距离最小值为1,则t的值为______;
(2)若点P在函数![]() 的图象上,且
的图象上,且![]() ,求h的最大值.
,求h的最大值.
【答案】(1)①![]() ;②
;②![]() 或
或![]() ;(2)2
;(2)2
【解析】
(1)①设解析式为![]() ,将
,将![]() 代入即可求解;
代入即可求解;
②当抛物线在x轴上方的点到x轴的距离为1时,y=1,
求出横坐标,即可知函数图象上点![]() 到x轴的距离最小值为1时
到x轴的距离最小值为1时![]() 的范围,于是可解;
的范围,于是可解;
(2)设解析式为![]() ,由
,由![]() 知图象过
知图象过![]() ,所以
,所以![]() .因为点P在函数
.因为点P在函数![]() 的图象上,所以
的图象上,所以![]() ,即
,即![]() ,分析增减趋势即可求出h的最大值.
,分析增减趋势即可求出h的最大值.
解:(1)①设解析式为![]() ,将
,将![]() 代入,
代入,
得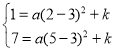 ,
,
解得![]() ,
,![]()
所以,解析式为![]() ,即
,即![]()
②抛物线![]() 的顶点为(3,-1),所以抛物线在x轴下方的点到x轴的最大距离为1,不符合题意;
的顶点为(3,-1),所以抛物线在x轴下方的点到x轴的最大距离为1,不符合题意;
当抛物线在x轴上方的点到x轴的距离为1时,y=1,
即![]() ,
,
解得,![]() ,
,
所以![]() 或
或![]() ,函数图象上点
,函数图象上点![]() 到x轴的距离最小值为1,
到x轴的距离最小值为1,
所以![]() 或
或![]() .
.
(2)设解析式为![]() ,由
,由![]() 知图象过
知图象过![]() ,所以
,所以![]() .
.
因为点P在函数![]() 的图象上,所以
的图象上,所以![]()
所以![]() ,
,
因为![]() ,所以
,所以![]()
因为![]() ,h随a的增大而减小,
,h随a的增大而减小,
所以,当![]() 时,h的值最大,h的最大值为2.
时,h的值最大,h的最大值为2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
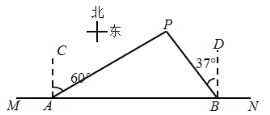
【题目】如图,船A、B在东西方向的海岸线MN上,均收到已触礁搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,在船B的北偏西37°方向上,AP=30海里.若船A、船B分别以20海里/时、15海里/时的速度同时出发,匀速直线前往救援,试通过计算判断哪艘船先到达船P处.(参考数据:sin37°≈0.60,cos37°≈0.80, tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
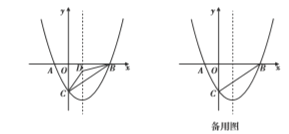
(1)求点![]() 三点的坐标和抛物线的对称轴;
三点的坐标和抛物线的对称轴;
(2)点![]() 为抛物线对称轴上一点,连接
为抛物线对称轴上一点,连接![]() ,
,![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)已知点![]() ,若
,若![]() 是抛物线上一个动点(其中
是抛物线上一个动点(其中![]() ),连接
),连接![]() ,
,![]() ,
,![]() ,求
,求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车产业的发展,有效促进我国现代化建设.某汽车销售公司2016年盈利1500万元,到2018年盈利2160万元,且从2016年到2018年,每年盈利的年增长率相同.
(1)求每年盈利的年增长率;
(2)若该公司盈利的年增长率继续保持不变,那么2019年该公司盈利能否达到2500万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有5个分别标有数字1,2,3,4,5的小球,它们的形状、大小、质地等完全相同.雄威同学先从盒子里随机取出第一个小球,记下数字为x;不放回盒子,再由丽贤同学随机取出第二个小球,记下数字为y.
(1)请用树状图或列表法表示出坐标(x,y)的所有可能出现的结果;
(2)求雄威同学、丽贤同学各取一个小球所确定的点(x,y)落在反比例函数y=![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
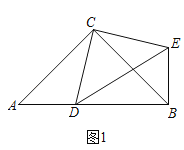
如图1,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=45°,点D时线段AB上一动点,连接BE.
填空:①![]() 的值为 ; ②∠DBE的度数为 .
的值为 ; ②∠DBE的度数为 .
(2)类比探究
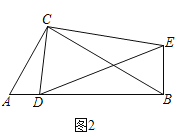
如图2,在Rt△ABC和Rt△CDE中,∠ACB=∠DCE=90°,∠CAB=∠CDE=60°,点D是线段AB上一动点,连接BE.请判断![]() 的值及∠DBE的度数,并说明理由;
的值及∠DBE的度数,并说明理由;
(3)拓展延伸
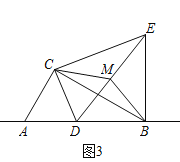
如图3,在(2)的条件下,将点D改为直线AB上一动点,其余条件不变,取线段DE的中点M,连接BM、CM,若AC=2,则当△CBM是直角三角形时,线段BE的长是多少?请直接写出答案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com