
【题目】中华文化,源远流长,在文学方面,《西游记》《三国演义》《水浒传》《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查.根据调查结果绘制成如所示的两个不完整的统计图,请结合图中信息解决下列问题:
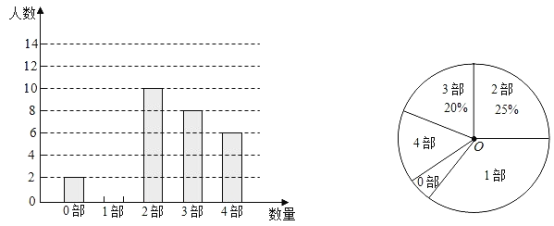
(1)请补全条形分布直方图,本次调查一共抽取了 名学生;
(2)扇形统计图中“1部”所在扇形的圆心角为 度;
(3)若该中学有1000名学生,请估计至少阅读3部四大古典名著的学生有多少名?
【答案】(1)补全图形见解析;40;(2)126;(3)350名
【解析】
(1)用2部人数除以其所占百分比即可得到总人数,总人数减去0、2、3、4部的人数即可求出1部的人数,然后补全图形即可;
(2)用360°乘以1部人数所占的百分比即可;
(3)用总人数乘以样本中3、4部人数占被调查人数的百分比即可.
解:(1)本次调查的总人数为10÷25%=40(人),
则“1部”的人数为40﹣(2+10+8+6)=14(人),
补全图形如下:
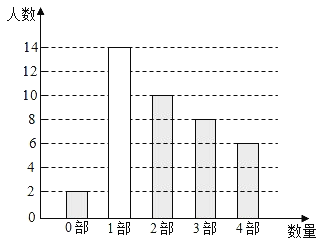
故答案为40;
(2)扇形统计图中“1部”所在扇形的圆心角为360°×![]() =126°,
=126°,
故答案为126;
(3)估计至少阅读3部四大古典名著的学生有1000×![]() =350(人).
=350(人).


科目:初中数学 来源: 题型:
【题目】(背景知识)数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a–b|,线段AB的中点表示的数为![]() .
.
(问题情境)如图,数轴上点A表示的数为–2,点B表示的数为8,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.
设运动时间为t秒(t>0).
(综合运用)(1)填空:①A、B两点间的距离AB=__________,线段AB的中点表示的数为__________;
②用含t的代数式表示:t秒后,点P表示的数为__________;点Q表示的数为__________.
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=![]() AB;
AB;
(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
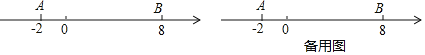
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,
以下各层均比上一层多一个圆圈,一共堆了n 层.将图1倒置后与原图1拼成图2的形状,这样我们可以
算出图1中所有圆圈的个数为1+2+3+…+n=![]() .
.

如果图中的圆圈共有13层,请解决下列问题:
(1)我们自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,……,则最底层最左
边这个圆圈中的数是 ;
(2)我们自上往下,在每个圆圈中按图4的方式填上一串连续的整数-23,-22,-21,-20,……,求
最底层最右边圆圈内的数是_______;
(3)求图4中所有圆圈中各数的绝对值之和.
查看答案和解析>>
科目:初中数学 来源: 题型:
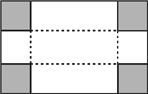
【题目】如图是一块矩形铁皮,将四个角各剪去一个边长为2米的正方形后,剩下的部分做成一个容积为90立方米的无盖长方体箱子,已知长方体箱子底面的长比宽多4米,求矩形铁皮的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
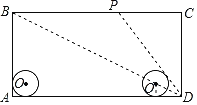
【题目】如图,在矩形ABCD中,AD=80cm,AB=40cm,半径为8cm的⊙O在矩形内且与AB、AD均相切.现有动点P从A点出发,在矩形边上沿着A→B→C→D的方向匀速移动,当点P到达D点时停止移动;⊙O在矩形内部沿AD向右匀速平移,移动到与CD相切时立即沿原路按原速返回,当⊙O回到出发时的位置(即再次与AB相切)时停止移动.已知点P与⊙O同时开始移动,同时停止移动(即同时到达各自的终止位置).当⊙O到达⊙O1的位置时(此时圆心O1在矩形对角线BD上),DP与⊙O1恰好相切,此时⊙O移动了( )cm.
A.56B.72C.56或72D.不存在
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点A,B,C为数轴上的三点,如果点C在点A,B之间,且到点A的距离是点C到点B的距离的3倍,那么我们就称点C是{A,B}的奇妙点.例如,如图①,点A表示的数为-3,点B表示的数为1.表示0的点C到点A的距离是3,到点B的距离是1,那么点C是{A,B}的奇妙点;又如,表示-2的点D到点A的距离是1,到点B的距离是3,那么点D就不是{A,B}的奇点,但点D是{B,A}的奇妙点.
(知识运用)
如图②,M,N为数轴上的两点,点M所表示的数为-2,点N所表示的数为6.
(1)表示数_____的点是{M,N}的奇妙点;表示数______的点是{N,M}的奇妙点;
(2)若点P所表示的数为3,点P是{M,N}的奇妙点,则点M、N所表示的数可以是几?M=______,N=_____(写出一组即可)
(3)如图③,A,B为数轴上的两点,点A所表示的数为-10,点B所表示的数为50.现有一动点P从点A出发向右运动,点P运动到数轴上的什么位置时,P,A,B中恰有一个点为其余两点的奇妙点?

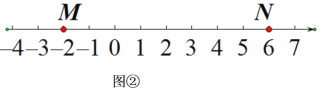
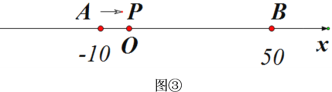
查看答案和解析>>
科目:初中数学 来源: 题型:
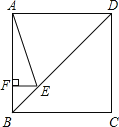
【题目】如图,正方形ABCD的边长为4,点E对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为点F,则EF的长为( )
A. 1B. 4-![]() C.
C. ![]() D.
D. ![]() -4
-4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
(1)小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是 ;
(2)小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区计划对面积为1600m2的区域进行绿化.经投标,由甲、乙两个工程队来完成,若甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍,并且在独立完成面积为400m2区域的绿化时,甲队比乙队少用5天.若甲队每天绿化费用是0.6万元,乙队每天绿化费用为0.25万元,规定甲乙两队单独施工的总天数不超过25天完成,且施工总费用最低,则最低费用为__________万元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com