(2002•荆州)已知半径为4和

的两圆相交,公共弦长为4,则两圆的圆心距为
.
【答案】
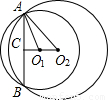
分析:设⊙O
1的半径为r=
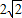
,⊙
2的半径为R=4,公共弦为AB,两圆的圆心的连线与公共弦的交点为C;那么根据相交两圆的定理,可出现来两个直角三角形,△O
1AC和△O
2AC,再利用勾股定理可求出O
1C和O
2C,就可求出O
1O
2.
解答: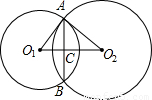
解:在Rt△O
1AC中,O
1C=
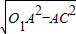
=
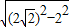
=2,
同理,在Rt△O
2AC中,O
2C=2
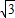
,
∴O
1O
2=O
1C+O
2C=2+2
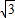
.
还有一种情况,O
1O
2=O
2C-O
1C=2
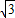
-2.
 点评:
点评:本题利用了相交两圆的定理,还用了勾股定理.
练习册系列答案
相关习题
科目:初中数学
来源:2002年全国中考数学试题汇编《二次函数》(03)(解析版)
题型:解答题
(2002•荆州)已知一抛物线与x轴的交点是A(-1,0)、B(m,0)且经过第四象限的点C(1,n),而m+n=-1,mn=-12,求此抛物线的解析式.
查看答案和解析>>
科目:初中数学
来源:2002年湖北省荆州市中考数学试卷(解析版)
题型:解答题
(2002•荆州)已知一抛物线与x轴的交点是A(-1,0)、B(m,0)且经过第四象限的点C(1,n),而m+n=-1,mn=-12,求此抛物线的解析式.
查看答案和解析>>
科目:初中数学
来源:2002年全国中考数学试题汇编《圆》(09)(解析版)
题型:填空题
(2002•荆州)已知半径为4和
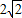
的两圆相交,公共弦长为4,则两圆的圆心距为
.
查看答案和解析>>
科目:初中数学
来源:2002年全国中考数学试题汇编《四边形》(05)(解析版)
题型:解答题
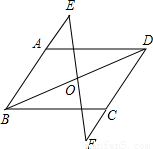
(2002•荆州)已知:如图,点O为?ABCD的对角线BD的中点,直线EF经过点O,分别交BA、DC的延长线于点E、F,求证:AE=CF.
查看答案和解析>>
科目:初中数学
来源:2002年全国中考数学试题汇编《三角形》(07)(解析版)
题型:解答题
(2002•荆州)已知:如图,点O为?ABCD的对角线BD的中点,直线EF经过点O,分别交BA、DC的延长线于点E、F,求证:AE=CF.

查看答案和解析>>

 的两圆相交,公共弦长为4,则两圆的圆心距为 .
的两圆相交,公共弦长为4,则两圆的圆心距为 .  新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
