
【题目】如图,正方形OABC和正方形CDEF在平面直角坐标系中,点O,C,F在y轴上,点O为坐标原点,点M为OC的中点,抛物线y=ax2+b经过M,B,E三点,则 ![]() 的值为 .
的值为 . 
【答案】1+ ![]()
【解析】解:设正方形OABC的边长为m,和正方形CDEF的边长为n.
∵点M为OC的中点,
∴点M为(0, ![]() )、点B为(m,m)和点E为(n,m+n),
)、点B为(m,m)和点E为(n,m+n),
∵抛物线y=ax2+b经过M,B,E三点,
∴m=am2+ ![]() ,
,
解得:a= ![]() ,
,
∴抛物线y= ![]() x2+
x2+ ![]() ,
,
把点E(n,m+n)代入抛物线得
m+n= ![]() n2+
n2+ ![]() ,
,
解得:n=m+ ![]() m或n=m﹣
m或n=m﹣ ![]() m(不合题意,舍去),
m(不合题意,舍去),
即CB=m,EF=m+ ![]() m,
m,
∴ ![]() =1+
=1+ ![]() .
.
设正方形OABC的边长为m,和正方形CDEF的边长为n.又点M为OC的中点,从而得出M,B,E三点的坐标,根据待定系数法求出抛物线的解析式,再把E点的坐标代入就可以得出用含m的式子表示n,从而表示出CB.EF的长度,进而得到其比值。


科目:初中数学 来源: 题型:
【题目】两组数据:98,99,99,100和98.5,99,99,99.5,则关于以下统计量说法不正确的是( )
A. 平均数相等
B. 中位数相等
C. 众数相等
D. 方差相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)某调查小组采用简单随机抽样方法,对某市部分中小学生一天中阳光体育运动时间进行了抽样调查,并把所得数据整理后绘制成如下的统计图:
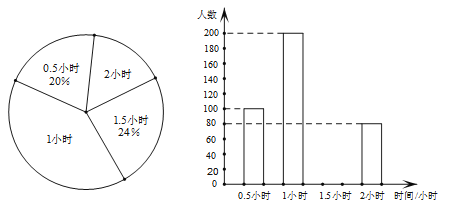
(1)该调查小组抽取的样本容量是多少?
(2)求样本学生中阳光体育运动时间为1.5小时的人数,并补全占频数分布直方图;
(3)请估计该市中小学生一天中阳光体育运动的平均时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校射击队从甲、乙、丙、丁四人中选拔一人参加市运动会射击比赛,在选拔比赛中,每人射击10次,他们10次成绩的平均数及方差如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数/环 | 9.5 | 9.5 | 9.6 | 9.6 |
方差/环2 | 5.1 | 4.7 | 4.5 | 5.1 |
请你根据表中数据选一人参加比赛,最合适的人选是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
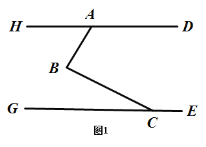
【题目】如图,直线![]() 点
点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 上,点
上,点![]() 在直线
在直线![]() 之间,
之间,![]()
![]() .
.
(1)如图1,若![]() ,求
,求![]() 的度数;
的度数;
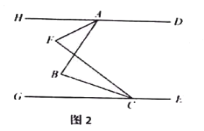
(2)如图2,![]() 平分
平分![]() 平分
平分![]() ,比较
,比较![]() 的大小;
的大小;
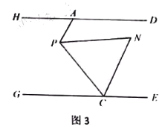
(3)如图3,点![]() 是线段
是线段![]() 上一点,
上一点,![]() 平分
平分![]() 平分
平分![]() ,探究
,探究![]() 和
和![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,直线AB:![]() 交y轴于点A(0,1),交x轴于点B.直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,且在点D的上方,设P(1,n).
交y轴于点A(0,1),交x轴于点B.直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,且在点D的上方,设P(1,n).
(1)求直线AB的解析式和点B的坐标;
(2)求△ABP的面积(用含n的代数式表示);
(3)当S△ABP=2时,以PB为边在第一象限作等腰直角三角形BPC,求出点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
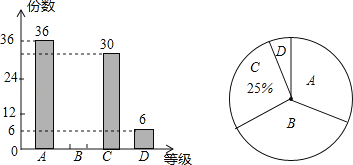
【题目】某校组织了主题为“让勤俭节约成为时尚”的电子小组作品征集活动,现从中随机抽取部分作品,按A,B,C,D四个等级进行评价,并根据结果绘制了如下两幅不完整的统计图.
(1)求抽取了多少份作品;
(2)此次抽取的作品中等级为B的作品有 ,并补全条形统计图;
(3)若该校共征集到800份作品,请估计等级为A的作品约有多少份.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理(解析)
提出问题:如图1,在四边形ABCD中,P是AD边上任意一点,△PBC与△ABC和△DBC的面积之间有什么关系?探究发现:为了解决这个问题,我们可以先从一些简单的、特殊的情形入手:
当AP=![]() AD时(如图2):
AD时(如图2):
∵AP=![]() AD,△ABP和△ABD的高相等,
AD,△ABP和△ABD的高相等,
∴S△ABP=![]() S△ABD,
S△ABD,
∵PD=AD﹣AP=![]() AD,△CDP和△CDA的高相等
AD,△CDP和△CDA的高相等
∴S△CDP=![]() S△CDA,
S△CDA,
∴S△PBC=S四边形ABCD﹣S△ABP﹣S△CDP=S四边形ABCD﹣![]() S△ABD﹣
S△ABD﹣![]() S△CDA,
S△CDA,
=S四边形ABCD﹣![]() (S四边形ABCD﹣S△DBC)﹣
(S四边形ABCD﹣S△DBC)﹣![]() (S四边形ABCD﹣S△ABC)=
(S四边形ABCD﹣S△ABC)=![]() S△DBC+
S△DBC+![]() S△ABC.
S△ABC.
(1)当AP=![]() AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;
AD时,探求S△PBC与S△ABC和S△DBC之间的关系式并证明;
(2)当AP=![]() AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
AD时,S△PBC与S△ABC和S△DBC之间的关系式为: ;
(3)一般地,当AP=![]() AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为: ;
AD(n表示正整数)时,探求S△PBC与S△ABC和S△DBC之间的关系为: ;
(4)当AP=![]() AD(0≤
AD(0≤![]() ≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .
≤1)时,S△PBC与S△ABC和S△DBC之间的关系式为: .

查看答案和解析>>
科目:初中数学 来源: 题型:
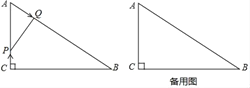
【题目】如图,已知Rt△ABC中,∠C=90°,∠A=60°,AC=3cm,AB=6m,点P在线段AC上以1cm/s的速度由点C向点A运动,同时,点Q在线段AB上以2cm/s的速度由点A向点B运动,设运动时间为t(s).
(1)当t=1时,判断△APQ的形状,并说明理由;
(2)当t为何值时,△APQ与△CQP全等?请写出证明过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com