
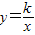 ��k��0����ͼ�����E��ֱ��l1�ཻ�ڵ�F��
��k��0����ͼ�����E��ֱ��l1�ཻ�ڵ�F��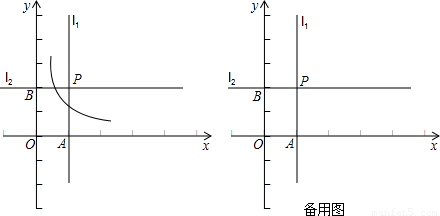
 k2-k+1������S��OEF=S����OCGD-S��DOF-S��EGF-S��OCE�������k��ֵ���������E�����ꣻ
k2-k+1������S��OEF=S����OCGD-S��DOF-S��EGF-S��OCE�������k��ֵ���������E�����ꣻ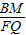 =
= �������BM��ֵ������Rt��MBE�У��ɹ��ɶ����ã�EM2=EB2+MB2�����k��ֵ�������ɵó�E�����꣮
�������BM��ֵ������Rt��MBE�У��ɹ��ɶ����ã�EM2=EB2+MB2�����k��ֵ�������ɵó�E�����꣮ PE•PF=
PE•PF= ��
��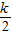 -1����k-2��=
-1����k-2��= k2-k+1��
k2-k+1��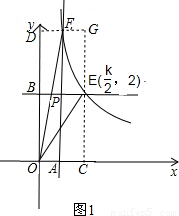
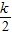 •k-
•k-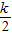 -��
-�� k2-k+1��-
k2-k+1��-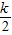 =
= k2-1
k2-1 k2-1=2��
k2-1=2�� k2-k+1����
k2-k+1����
 =
=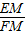 ��
�� ��FM=PF=2-k��
��FM=PF=2-k�� =
=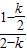 ��BM=
��BM= ��
��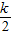 ��2=��
��2=��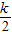 ��2+��
��2+�� ��2��
��2�� ����ʱE������Ϊ��
����ʱE������Ϊ�� ��2����
��2���� �ڵ�k��2ʱ����ͼ3��
�ڵ�k��2ʱ����ͼ3��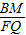 =
=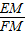 ��
�� -1��
-1��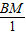 =
=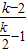 ��BM=2��
��BM=2��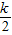 ��2+22�����k=
��2+22�����k=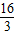 ��0����k=0���������⣬
��0����k=0���������⣬ ��
�� ��2����
��2���� ��2����
��2���� ��2����
��2����

 ���źþ���Ԫ����ĩ��ϵ�д�
���źþ���Ԫ����ĩ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����ƽ��ֱ������ϵxOy�У���ABC��A��B����������x���ϣ�����C��y��ĸ������ϣ���֪|OA|��|OB|=1��5��|OB|=|OC|����ABC�����S��ABC=15��������y=ax2+bx+c��a��0������A��B��C���㣮
��ͼ����ƽ��ֱ������ϵxOy�У���ABC��A��B����������x���ϣ�����C��y��ĸ������ϣ���֪|OA|��|OB|=1��5��|OB|=|OC|����ABC�����S��ABC=15��������y=ax2+bx+c��a��0������A��B��C���㣮| 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����ƽ��ֱ������ϵxOy�У�A��2��1����B��4��1����C��1��3�������ABC���ABDȫ�ȣ����D����Ϊ
��ͼ����ƽ��ֱ������ϵxOy�У�A��2��1����B��4��1����C��1��3�������ABC���ABDȫ�ȣ����D����Ϊ�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com