
 的图像交于M、N两点。
的图像交于M、N两点。
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案科目:初中数学 来源:不详 题型:解答题
 经过点A(1,0),与双曲线
经过点A(1,0),与双曲线 交于点B(2,1).过点P(
交于点B(2,1).过点P( ,
, -1)(其中
-1)(其中 >1)作
>1)作 轴的平行线分别交双曲线
轴的平行线分别交双曲线 和
和 于点M、N.
于点M、N.
 的值;
的值; 的解析式;
的解析式; ,使得S△AMN=4S△AMP?若存在,请求出所有满足条件的
,使得S△AMN=4S△AMP?若存在,请求出所有满足条件的 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图象与反比例函数
的图象与反比例函数 的图象的一个交点为A(1,m),点B(n,1)在反比例函数的图象上.
的图象的一个交点为A(1,m),点B(n,1)在反比例函数的图象上.
 轴上一点,且满足△POB的面积为6,求P点的坐标.
轴上一点,且满足△POB的面积为6,求P点的坐标.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
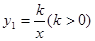 与直线
与直线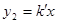 交于A,B两点,点A在第一象限.试解答下列问题:
交于A,B两点,点A在第一象限.试解答下列问题: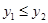 ;
;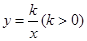 于P,Q两点,点P在第一象限, 如图2所示.
于P,Q两点,点P在第一象限, 如图2所示.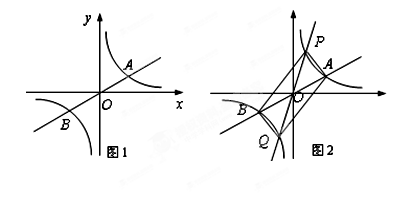
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
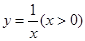 的图象上,△OP1A1,△P2A1A2,△P3A2A3……△PnAn-1An……都是等腰直角三角形,斜边OA1,A1A2……An-1An,都在x轴上, 则y1+y2+…yn= 。
的图象上,△OP1A1,△P2A1A2,△P3A2A3……△PnAn-1An……都是等腰直角三角形,斜边OA1,A1A2……An-1An,都在x轴上, 则y1+y2+…yn= 。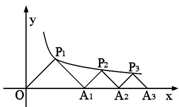
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com