
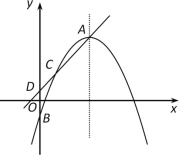
【题目】如图,在平面直角坐标系中,已知二次函数![]() 图象的顶点为A,与y轴交于点B,异于顶点A的点C(1,n)在该函数图象上.
图象的顶点为A,与y轴交于点B,异于顶点A的点C(1,n)在该函数图象上.
(1)当m=5时,求n的值.
(2)当n=2时,若点A在第一象限内,结合图象,求当y![]() 时,自变量x的取值范围.
时,自变量x的取值范围.
(3)作直线AC与y轴相交于点D.当点B在x轴上方,且在线段OD上时,求m的取值范围.
【答案】(1)-4(2)1≤x≤5(3)0≤m<1或1<m<2![]()
【解析】
1)利用待定系数法求解即可.
(2)求出![]() 时,
时,![]() 的值即可判断.
的值即可判断.
(3)由题意点![]() 的坐标为
的坐标为![]() ,求出几个特殊位置
,求出几个特殊位置![]() 的值即可判断.
的值即可判断.
解:(1)当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() .
.
(2)当![]() 时,将
时,将![]() 代入函数表达式
代入函数表达式![]() ,得
,得![]() ,
,
解得![]() 或
或![]() (舍弃),
(舍弃),
![]() 此时抛物线的对称轴
此时抛物线的对称轴![]() ,
,
根据抛物线的对称性可知,当![]() 时,
时,![]() 或5,
或5,
![]() 的取值范围为
的取值范围为![]() .
.
(3)![]() 点
点![]() 与点
与点![]() 不重合,
不重合,
![]() ,
,
![]() 抛物线的顶点
抛物线的顶点![]() 的坐标是
的坐标是![]() ,
,
![]() 抛物线的顶点在直线
抛物线的顶点在直线![]() 上,
上,
当![]() 时,
时,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,
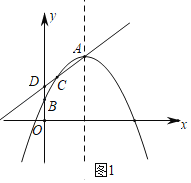
抛物线从图1的位置向左平移到图2的位置,![]() 逐渐减小,点
逐渐减小,点![]() 沿
沿![]() 轴向上移动,
轴向上移动,
当点![]() 与
与![]() 重合时,
重合时,![]() ,
,
解得![]() 或
或![]() ,
,
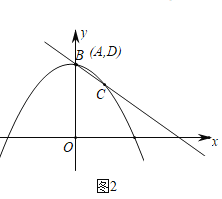
当点![]() 与点
与点![]() 重合时,如图2,顶点
重合时,如图2,顶点![]() 也与
也与![]() ,
,![]() 重合,点
重合,点![]() 到达最高点,
到达最高点,
![]() 点
点![]() ,
,
![]() ,解得
,解得![]() ,
,
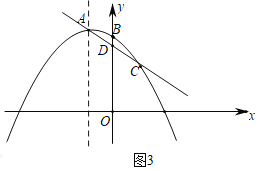
当抛物线从图2的位置继续向左平移时,如图3点![]() 不在线段
不在线段![]() 上,
上,
![]() 点在线段
点在线段![]() 上时,
上时,![]() 的取值范围是:
的取值范围是:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
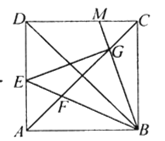
【题目】如图,在边长为6的正方形ABCD中,点E为边AD上的一个动点(与点A,D不重合),![]() ,BE交对角线AC于点F,BM交于AC于点G,交CD于点M.
,BE交对角线AC于点F,BM交于AC于点G,交CD于点M.
(1)求DE:CG的值;
(2)设![]() ,
,![]() ,
,
①求y关于x的函数表达式及x的取值范围.
②当图中点E,M关于对角线BD成轴对称时,求y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.“掷一次骰子,向上一面的点数是![]() ”是必然事件
”是必然事件
B.掷一枚硬币正面朝上的概率是![]() 表示每抛硬币
表示每抛硬币![]() 次就有
次就有![]() 次正面朝上
次正面朝上
C.计算甲组和乙组数据,得知![]() ,
,![]() ,
,![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
D.一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的众数和中位数都是
的众数和中位数都是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
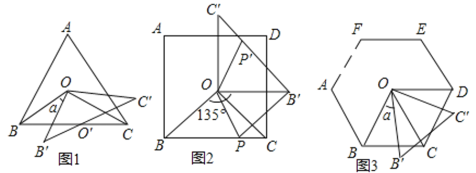
【题目】在下列正多边形中,![]() 是中心,定义:
是中心,定义:![]() 为相应正多边形的基本三角形.如图1,
为相应正多边形的基本三角形.如图1,![]() 是正三角形
是正三角形![]() 的基本三角形;如图2,
的基本三角形;如图2,![]() 是正方形
是正方形![]() 的基本三角形;如图3,
的基本三角形;如图3,![]() 为正
为正![]() 边形
边形![]() …的基本三角形.将基本
…的基本三角形.将基本![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 角度得
角度得![]() .
.
(1)若线段![]() 与线段
与线段![]() 相交点
相交点![]() ,则:
,则:
图1中![]() 的取值范围是________;
的取值范围是________;
图3中![]() 的取值范围是________;
的取值范围是________;
(2)在图1中,求证![]()
(3)在图2中,正方形边长为4,![]() ,边
,边![]() 上的一点
上的一点![]() 旋转后的对应点为
旋转后的对应点为![]() ,若
,若![]() 有最小值时,求出该最小值及此时
有最小值时,求出该最小值及此时![]() 的长度;
的长度;
(4)如图3,当![]() 时,直接写出
时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
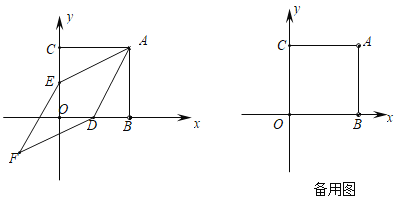
【题目】如图,在平面直角坐标系中,正方形ABOC的两直角边分别在坐标轴的正半轴上,分别过OB,OC的中点D,E作AE,AD的平行线,相交于点F, 已知OB=8.
(1)求证:四边形AEFD为菱形.
(2)求四边形AEFD的面积.
(3)若点P在x轴正半轴上(异于点D),点Q在y轴上,平面内是否存在点G,使得以点A,P, Q,G为顶点的四边形与四边形AEFD相似?若存在,求点P的坐标;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
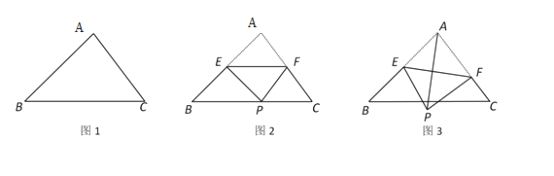
【题目】如图,在△ABC中,AB=![]() ,∠B=45°,∠C=60°.
,∠B=45°,∠C=60°.
(1)求BC边上的高线长.
(2)点E为线段AB的中点,点F在边AC上,连结EF,沿EF将△AEF折叠得到△PEF.
①如图2,当点P落在BC上时,求∠AEP的度数.
②如图3,连结AP,当PF⊥AC时,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,BD的垂直平分线交AD于E,交BC于F,连接BE 、DF.

(1)判断四边形BEDF的形状,并说明理由;
(2)若AB=8,AD=16,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
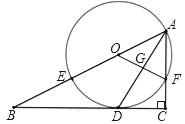
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是⊙O的切线;
(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;
(3)若BE=8,sinB=![]() ,求DG的长,
,求DG的长,
查看答案和解析>>
科目:初中数学 来源: 题型:
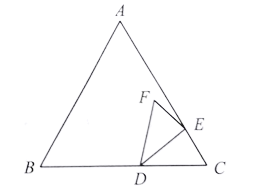
【题目】如图,等边三角形![]() 中,
中,![]() 点
点![]() 在边
在边![]() 上,
上,![]() .点
.点![]() 为边
为边![]() 上一动点(不与点
上一动点(不与点![]() 重合),连接
重合),连接![]() 关于
关于![]() 的轴对称图形为
的轴对称图形为![]() .
.
(1)当点![]() 在
在![]() 上时,求证:
上时,求证:![]() ;
;
(2)当![]() 三点共线时,求
三点共线时,求![]() 的长;
的长;
(3)连接![]() 设
设![]() 的面积为
的面积为![]() 的面积为
的面积为![]() 记
记![]()
![]() 是否存在最大值?若存在,请直接写出
是否存在最大值?若存在,请直接写出![]() 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com