
【题目】将一个矩形纸片![]() 放置在平面直角坐标系中,点
放置在平面直角坐标系中,点![]() 点
点![]() 点
点![]()
![]() 是边
是边![]() 上的一点(点
上的一点(点![]() 不与点
不与点![]() 重合),沿着
重合),沿着![]() 折叠该纸片,得点
折叠该纸片,得点![]() 的对应点
的对应点![]() .
.
(1)如图①,当点![]() 落在边
落在边![]() 上时,求点
上时,求点![]() 的坐标;
的坐标;

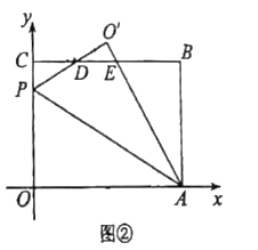
(2)若点![]() 落在边
落在边![]() 的上方,
的上方,![]() 与分别与边
与分别与边![]() 交于点
交于点![]() .
.
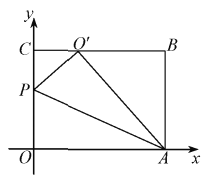
①如图②,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
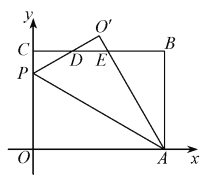
②当![]() 时,求点
时,求点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
【答案】(1)点![]() 的坐标为
的坐标为![]() ;(2)①
;(2)①![]() ,②(
,②(![]() ,6).
,6).
【解析】
(1)根据矩形和折叠性质可知![]() ,
,![]() ,然后利用勾股定理求得
,然后利用勾股定理求得![]() ,从而求得
,从而求得![]() ,由此确定点
,由此确定点![]() 的坐标;
的坐标;
(2)①根据折叠的性质求得![]() ,然后解直角三角形求得
,然后解直角三角形求得![]() ,CD=
,CD=![]() ,从而确定D点坐标;
,从而确定D点坐标;
②根据角边角定理证得△CPD≌△![]() ,从而求得
,从而求得![]() ,然后设P(0,m),则
,然后设P(0,m),则![]() ,
,![]() ,
,![]() ,
,![]() ,利用勾股定理列方程求得m的值,从而求得
,利用勾股定理列方程求得m的值,从而求得![]() ,设CD=x,则
,设CD=x,则![]() ,再用勾股定理列方程求x的值,从而求得D点坐标.
,再用勾股定理列方程求x的值,从而求得D点坐标.
解:(1)∵点![]() ,点
,点![]() 为矩形,
为矩形,
![]()
根据题意,由折叠可知![]()
![]()
在![]() 中,
中,![]()
![]()
![]() 点
点![]() 的坐标为
的坐标为![]()
(2)①![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
∴在Rt△AOP中,![]()
![]()
在Rt△CPD中,![]() ,
,
∴CD=![]()
∴D点坐标为(![]() ,6)
,6)
②当![]() 时,
时,
∵![]() ,
,![]()
∴△CPD≌△![]()
∴DE=DP
∴![]()
设P(0,m),则![]() ,
,![]() ,
,![]()
∴![]()
∴在Rt△ABE中,![]() ,解得:m=
,解得:m=![]()
∴![]()
设CD=x,则![]()
∴在Rt△CPD中,![]() ,解得
,解得![]()
∴D点坐标为(![]() ,6).
,6).


科目:初中数学 来源: 题型:
【题目】某大学生利用业余时间参与了一家网店经营,销售一种成本为30元/件的文化衫,根据以往的销售经验,他整理出这种文化衫的售价y1(元/件),销量y2(件)与第x(1≤x<90)天的函数图象如图所示(销售利润=(售价-成本)×销量).
(1)求y1与y2的函数解析式.
(2)求每天的销售利润W与x的函数解析式.
(3)销售这种文化衫的第多少天,销售利润最大,最大利润是多少?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,且经过
,且经过![]() ,
,![]() 两点,点
两点,点![]() 是抛物线顶点,
是抛物线顶点,![]() 是对称轴与直线
是对称轴与直线![]() 的交点,
的交点,![]() 与
与![]() 关于点
关于点![]() 对称.
对称.
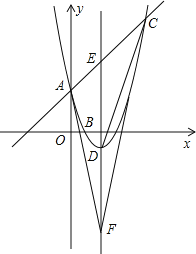
(1)求抛物线的解析式;
(2)求证:![]() ;
;
(3)在抛物线的对称轴上是否存在点![]() ,使
,使![]() 与
与![]() 相似.若有,请求出所有符合条件的点
相似.若有,请求出所有符合条件的点![]() 的坐标;若没有,请说明理由.
的坐标;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某儿童游乐园推出两种门票收费方式:
方式一:购买会员卡,每张会员卡费用是![]() 元,凭会员卡可免费进园
元,凭会员卡可免费进园![]() 次,免费次数用完以后,每次进园凭会员卡只需
次,免费次数用完以后,每次进园凭会员卡只需![]() 元;
元;
方式二:不购买会员卡,每次进园是![]() 元(两种方式每次进园均指单人)设进园次数为
元(两种方式每次进园均指单人)设进园次数为![]() (
( ![]() 为非负整数) .
为非负整数) .
(1)根据题意,填写下表:
进园次数(次) |
|
|
| ··· |
方式一收费(元) |
|
| ··· | |
方式二收费(元) |
| ··· |
(2)设方式一收费![]() 元,方式二收费
元,方式二收费![]() 元,分别写出
元,分别写出关于
![]() 的函数关系式;;
的函数关系式;;
(3)当![]() 时,哪种进园方式花费少?请说明理由.
时,哪种进园方式花费少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
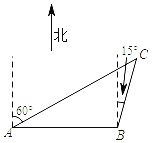
【题目】在一次综合社会实践活动中,小东同学从A处出发,要到A地北偏东60°方向的C处,他先沿正东方向走了4千米到达B处,再沿北偏东15°方向走,恰能到达目的地C,如图所示,则A、C两地相距__千米.(结果精确到0.1千米,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面内有一点P到△ABC的三个顶点的距离分别为PA、PB、PC,若有PA2+PB2=PC2,则称点P为△ABC关于点C的勾股点.

(1)如图2,在4×3的方格纸中,每个小正方形的边长均为1,△ABC的顶点在格点上,请找出所有的格点P,使点P为△ABC关于点A的勾股点.
(2)如图3,△ABC为等腰直角三角形,P是斜边BC延长线上一点,连接AP,以AP为直角边作等腰直角三角形APD(点A、P、D顺时针排列)∠PAD=90°,连接DC,DB,求证:点P为△BDC关于点D的勾股点.
(3)如图4,点E是矩形ABCD外一点,且点C是△ABE关于点A的勾股点,若AD=8,CE=5,AD=DE,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在菱形ABCD中.(1)分别以C,D为圆心,大于![]() 长为半径作弧,两弧分别交于点E,F;(2)作直线EF,且直线EF恰好经过点A,且与边CD交于点M;(3)连接BM.根据以上作图过程及所作图形,判断下列结论中错误的是( )
长为半径作弧,两弧分别交于点E,F;(2)作直线EF,且直线EF恰好经过点A,且与边CD交于点M;(3)连接BM.根据以上作图过程及所作图形,判断下列结论中错误的是( )

A.∠ABC=60°B.如果AB=2,那么BM=4
C.BC=2CMD.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com