
【题目】小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(计算结果精确到1m) (参考数据:sin15°= ![]() ,cos15°=
,cos15°= ![]() ,tan15°=
,tan15°= ![]() )
)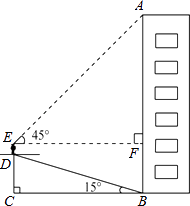
【答案】解:作DH⊥AB于H, ∵∠DBC=15°,BD=20,
∴BC=BDcos∠DBC=20× ![]() =19.2,CD=BDsin∠DBC=20×
=19.2,CD=BDsin∠DBC=20× ![]() =5,
=5,
由题意得,四边形ECBF和四边形CDHB是矩形,
∴EF=BC=19.2,BH=CD=5,
∵∠AEF=45°,
∴AF=EF=19.2,
∴AB=AF+FH+HB=19.2+1.6+5=25.8≈26m,
答:楼房AB的高度约为26m.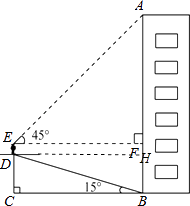
【解析】作DH⊥AB于H,根据余弦的定义求出BC,根据正弦的定义求出CD,结合题意计算即可.
【考点精析】解答此题的关键在于理解关于坡度坡角问题的相关知识,掌握坡面的铅直高度h和水平宽度l的比叫做坡度(坡比).用字母i表示,即i=h/l.把坡面与水平面的夹角记作A(叫做坡角),那么i=h/l=tanA,以及对关于仰角俯角问题的理解,了解仰角:视线在水平线上方的角;俯角:视线在水平线下方的角.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系内,小正方形网格的边长为1个单位长度,△ABC的三个顶点的坐标分别为A(﹣1,3),B(﹣4,0),C(0,0)
(1)画出将△ABC向上平移1个单位长度,再向右平移5个单位长度后得到的△A1B1C1;
(2)画出将△ABC绕原点O顺时针方向旋转90°得到△A2B2O;
(3)在x轴上存在一点P,满足点P到A1与点A2距离之和最小,请直接写出P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB,AD与⊙O相切于点B,D,C为⊙O上一点,且∠BCD=140°,则∠A的度数是( ) 
A.70°
B.105°
C.100°
D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究.探究过程如下,请补充完整. 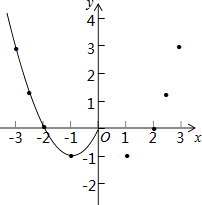
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | n |
| 3 | … |
其中,m= , n= .
(2)根据表格数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该图象的另一部分.
(3)观察函数图象,写出两条函数的性质:①;② .
(4)进一步探究函数图象发现: ①函数图象与x轴有个交点,所以对应的方程x2﹣2|x|=0有个实数根;
②方程x2﹣2|x|=2有个实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D是BC上一点,∠DAC=∠B,E为AB上一点. 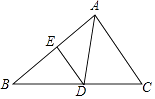
(1)求证:△CAD∽△CBA;
(2)若BD=10,DC=8,求AC的长;
(3)在(2)的条件下,若DE∥AC,AE=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁4位同学进行一次乒乓球单打比赛,要从中选2名同学打第一场比赛.
(1)已确定甲同学打第一场比赛,再从其余3名同学中随机选取1名,恰好选中乙同学的概率是多少?;
(2)随机选取2名同学,求其中有乙同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高22米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上).
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈ ![]() ,cos22°≈
,cos22°≈ ![]() ,tan22≈
,tan22≈ ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com