
如图,已知二次函数L1:y=x2-4x+3与x轴交于A.B两点(点A在点B左边),与y轴交于点C.

(1)写出二次函数L1的开口方向、对称轴和顶点坐标;
(2)研究二次函数L2:y=kx2-4kx+3k(k≠0).
①写出二次函数L2与二次函数L1有关图象的两条相同的性质;
②若直线y=8k与抛物线L2交于E、F两点,问线段EF的长度是否发生变化?如果不会,请求出EF的长度;如果会,请说明理由.
|
分析:(1)抛物线y=ax2+bx+c中:a的值决定了抛物线的开口方向,a>0时,抛物线的开口向上;a<0时,抛物线的开口向下. 抛物线的对称轴方程:x=- (2)①新函数是由原函数的各项系数同时乘以k所得,因此从二次函数的图象与解析式的系数的关系入手进行分析. ②联系直线和抛物线L2的解析式,先求出点E、F的坐标,进而可表示出EF的长,若该长度为定值,则线段EF的长不会发生变化. 解答:解:(1)抛物线y=x2-4x+3中,a=1、b=-4、c=3; ∴- ∴二次函数L1的开口向上,对称轴是直线x=2,顶点坐标(2,-1). (2)①二次函数L2与L1有关图象的两条相同的性质: 对称轴为x=2或定点的横坐标为2, 都经过A(1,0),B(3,0)两点; ②线段EF的长度不会发生变化. ∵直线y=8k与抛物线L2交于E、F两点, ∴kx2-4kx+3k=8k, ∵k≠0,∴x2-4x+3=8, 解得:x1=-1,x2=5,∴EF=x2-x1=6, ∴线段EF的长度不会发生变化.
点评:该题主要考查的是函数的基础知识,有:二次函数的性质、函数图象交点坐标的解法等,难度不大,但需要熟练掌握. |
|
二次函数综合题. |


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:
| 5 |
| 2 |
| 13 |
| 4 |
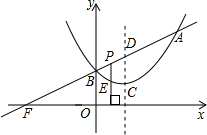 三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.
三角形与△BOF相似?若存在,请求出P点的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
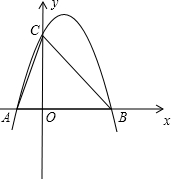
查看答案和解析>>
科目:初中数学 来源: 题型:
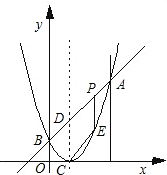 如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.
如图,已知二次函数图象的顶点坐标为C(1,0),直线y=x+b与该二次函数的图象交于A、B两点,其中点A的坐标为(3,4),点B在y轴上.点P为线段AB上的一个动点(点P与A、B不重合),过点P作x轴的垂线与该二次函数的图象交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:
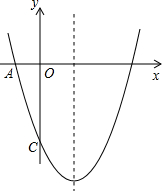 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点C(0,-5).查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•衡水一模)如图,已知二次函数y=-
(2012•衡水一模)如图,已知二次函数y=-| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com