
”¾ĢāÄæ”æŅŃÖŖŅ»“ĪŗÆŹż![]() ŗĶ·“±ČĄżŗÆŹż
ŗĶ·“±ČĄżŗÆŹż![]() £®
£®
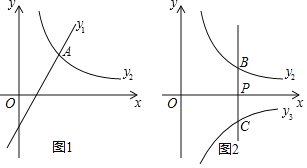
£Ø1£©ČēĶ¼1£¬Čō![]() £¬ĒŅŗÆŹż
£¬ĒŅŗÆŹż![]() ”¢
”¢![]() µÄĶ¼Ļ󶼾¹żµć
µÄĶ¼Ļ󶼾¹żµć![]() £®
£®
¢ŁĒó![]() £¬
£¬![]() µÄÖµ£»
掙术
¢ŚÖ±½ÓŠ“³öµ±![]() Ź±
Ź±![]() µÄ·¶Ī§£»
µÄ·¶Ī§£»
£Ø2£©ČēĶ¼2£¬¹żµć![]() ×÷
×÷![]() ÖįµÄĘ½ŠŠĻß
ÖįµÄĘ½ŠŠĻß![]() ÓėŗÆŹż
ÓėŗÆŹż![]() µÄĶ¼ĻóĻą½»ÓŚµć
µÄĶ¼ĻóĻą½»ÓŚµć![]() £¬Óė·“±ČĄżŗÆŹż
£¬Óė·“±ČĄżŗÆŹż![]() µÄĶ¼ĻóĻą½»ÓŚµć
µÄĶ¼ĻóĻą½»ÓŚµć![]() £®
£®
¢ŁČō![]() £¬Ö±Ļß
£¬Ö±Ļß![]() ÓėŗÆŹż
ÓėŗÆŹż![]() µÄĶ¼ĻóĻą½»µć
µÄĶ¼ĻóĻą½»µć![]() £®µ±µć
£®µ±µć![]() ”¢
Ӣ![]() Ӣ
”¢![]() ÖŠµÄŅ»µćµ½ĮķĶāĮ½µćµÄ¾ąĄėĻąµČŹ±£¬Ēó
ÖŠµÄŅ»µćµ½ĮķĶāĮ½µćµÄ¾ąĄėĻąµČŹ±£¬Ēó![]() µÄÖµ£»
掙术
¢Ś¹żµć![]() ×÷
×÷![]() ÖįµÄĘ½ŠŠĻßÓėŗÆŹż
ÖįµÄĘ½ŠŠĻßÓėŗÆŹż![]() µÄĶ¼ĻóĻą½»ÓŚµć
µÄĶ¼ĻóĻą½»ÓŚµć![]() £®µ±
£®µ±![]() µÄֵȔ²»“óÓŚ1µÄČĪŅāŹµŹżŹ±£¬µć
µÄֵȔ²»“óÓŚ1µÄČĪŅāŹµŹżŹ±£¬µć![]() ”¢
”¢![]() ¼äµÄ¾ąĄėÓėµć
¼äµÄ¾ąĄėÓėµć![]() ”¢
”¢![]() ¼äµÄ¾ąĄėÖ®ŗĶ
¼äµÄ¾ąĄėÖ®ŗĶ![]() Ź¼ÖÕŹĒŅ»øö¶ØÖµ£®Ēó“ĖŹ±
Ź¼ÖÕŹĒŅ»øö¶ØÖµ£®Ēó“ĖŹ±![]() µÄÖµ¼°¶ØÖµ
µÄÖµ¼°¶ØÖµ![]() £®
£®
”¾“š°ø”æ£Ø1£©¢Ł![]() £¬
£¬![]() £»¢Ś
£»¢Ś![]() £»£Ø2£©¢Ł
£»£Ø2£©¢Ł![]() »ņ4£»¢Ś
»ņ4£»¢Ś![]() £¬
£¬![]() £®
£®
”¾½āĪö”æ
£Ø1£©¢Ł½«µć![]() µÄ×ų±ź“śČėŅ»“ĪŗÆŹż±ķ“ļŹ½¼“æÉĒó½ā£¬½«µć
µÄ×ų±ź“śČėŅ»“ĪŗÆŹż±ķ“ļŹ½¼“æÉĒó½ā£¬½«µć![]() µÄ×ų±ź“śČė·“±ČĄżŗÆŹż±ķ“ļŹ½£¬¼“æÉĒó½ā£»¢ŚÓÉĶ¼ĻóæÉŅŌÖ±½Ó擳ö£»
µÄ×ų±ź“śČė·“±ČĄżŗÆŹż±ķ“ļŹ½£¬¼“æÉĒó½ā£»¢ŚÓÉĶ¼ĻóæÉŅŌÖ±½Ó擳ö£»
£Ø2£©¢Ł![]() £¬
£¬![]() £¬
£¬![]() £¬ÓÉ
£¬ÓÉ![]() »ņ
»ņ![]() »ņ
»ņ![]() µĆ£ŗ
µĆ£ŗ![]() »ņ0»ņ2£¬¼“æÉĒó½ā£»¢Śµć
»ņ0»ņ2£¬¼“æÉĒó½ā£»¢Śµć![]() µÄ×ų±źĪŖ
µÄ×ų±źĪŖ![]() £¬
£¬![]()
![]() £¬¼“æÉĒó½ā£®
£¬¼“æÉĒó½ā£®
£Ø1£©¢Ł½«µć![]() µÄ×ų±ź“śČėŅ»“ĪŗÆŹż±ķ“ļŹ½²¢½āµĆ£ŗ
µÄ×ų±ź“śČėŅ»“ĪŗÆŹż±ķ“ļŹ½²¢½āµĆ£ŗ![]() £¬
£¬
½«µć![]() µÄ×ų±ź“śČė·“±ČĄżŗÆŹżµĆ£ŗ
µÄ×ų±ź“śČė·“±ČĄżŗÆŹżµĆ£ŗ![]() £»
£»
¢ŚÓÉĶ¼ĻóæÉŅŌ擳ö![]() Ź±£¬
Ź±£¬![]() £»
£»
£Ø2£©¢Łµ±![]() Ź±£¬µć
Ź±£¬µć![]() ”¢
Ӣ![]() Ӣ
”¢![]() µÄ×ų±ź·Ö±šĪŖ
µÄ×ų±ź·Ö±šĪŖ![]() ”¢
Ӣ![]() Ӣ
”¢![]() £¬
£¬
Ōņ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬
Ōņ![]() »ņ
»ņ![]() »ņ
»ņ![]() £¬
£¬
¼“£ŗ![]() »ņ
»ņ![]() »ņ
»ņ![]() £¬
£¬
¼“£ŗ![]() »ņ0»ņ2»ņ4£¬
»ņ0»ņ2»ņ4£¬
µ±![]() Ź±£¬
Ź±£¬![]() ÓėĢāŅā²»·ū£¬
ÓėĢāŅā²»·ū£¬
µć![]() ²»ÄÜŌŚ
²»ÄÜŌŚ![]() µÄĻĀ·½£¬¼“
µÄĻĀ·½£¬¼“![]() Ņ²²»“ęŌŚ£¬
Ņ²²»“ęŌŚ£¬![]() £¬¹Ź
£¬¹Ź![]() ²»³ÉĮ¢£¬
²»³ÉĮ¢£¬
¹Ź![]() »ņ4£»
»ņ4£»
¢Śµć![]() µÄŗį×ų±źĪŖ£ŗ
µÄŗį×ų±źĪŖ£ŗ![]() £¬
£¬
µ±µć![]() ŌŚµć
ŌŚµć![]() ×ó²ąŹ±£¬
×ó²ąŹ±£¬
![]()
![]() £¬
£¬
![]() µÄֵȔ²»“óÓŚ1µÄČĪŅāŹżŹ±£¬
µÄֵȔ²»“óÓŚ1µÄČĪŅāŹżŹ±£¬![]() Ź¼ÖÕŹĒŅ»øö¶ØÖµ£¬
Ź¼ÖÕŹĒŅ»øö¶ØÖµ£¬
µ±![]() Ź±£¬“ĖŹ±
Ź±£¬“ĖŹ±![]() £¬“Ó¶ų
£¬“Ó¶ų![]() £®
£®
µ±µć![]() ŌŚµć
ŌŚµć![]() ÓŅ²ąŹ±£¬
ÓŅ²ąŹ±£¬
Ķ¬Ąķ![]() £¬
£¬
µ±![]() £¬
£¬![]() Ź±£¬£Ø²»ŗĻĢāŅāÉįČ„£©
Ź±£¬£Ø²»ŗĻĢāŅāÉįČ„£©
¹Ź![]() £¬
£¬![]() £®
£®



 Ļ°Ģā¾«Ń”ĻµĮŠ“š°ø
Ļ°Ģā¾«Ń”ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČōÅ×ĪļĻߵĶ„µć×ų±źŹĒ![]() £¬²¢ĒŅÅ×ĪļĻßÓė
£¬²¢ĒŅÅ×ĪļĻßÓė![]() ÖįĮ½½»µć¼äµÄ¾ąĄėĪŖ8£¬ŹŌĒóøĆÅ×ĪļĻߵĹŲĻµŹ½£¬²¢Ēó³öÕāĢõÅ×ĪļĻßÉĻׯ×ų±źĪŖ10µÄµćµÄ×ų±ź”£
ÖįĮ½½»µć¼äµÄ¾ąĄėĪŖ8£¬ŹŌĒóøĆÅ×ĪļĻߵĹŲĻµŹ½£¬²¢Ēó³öÕāĢõÅ×ĪļĻßÉĻׯ×ų±źĪŖ10µÄµćµÄ×ų±ź”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
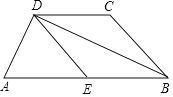
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬ŌŚĢŻŠĪABCDÖŠ£¬AB”ĪCD£¬BC£½CD£¬AD”ĶBD£¬EĪŖABÖŠµć£®
£Ø1£©ĒóÖ¤£ŗĖıߊĪBCDEŹĒĮāŠĪ£®
£Ø2£©ČōAD£½6£¬BD£½8£¬ĒóĖıߊĪBCDEµÄÖܳ¤ŗĶĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
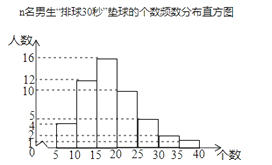
”¾ĢāÄæ”æijŠ£ĪŖĮĖŌ¤²ā¾ÅÄź¼¶ÄŠÉś”°ÅÅĒņ30Ćė”±¶ŌĒ½µęĒņµÄĒéæö£¬“Ó±¾Š£¾ÅÄź¼¶Ė껜³éČ”ĮĖnĆūÄŠÉś½ųŠŠøĆĻīÄæ²āŹŌ£¬²¢»ęÖĘ³öČēĻĀµÄʵŹż·Ö²¼Ö±·½Ķ¼£¬ĘäÖŠ“Ó×óµ½ÓŅŅĄ“Ī·ÖĪŖĘßøö×é£ØĆæ×éŗ¬×īŠ”Öµ£¬²»ŗ¬×ī“óÖµ£©£®øł¾ŻĶ³¼ĘĶ¼Ģį¹©µÄŠÅĻ¢½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©ĒónµÄÖµ£®
£Ø2£©ÕāøöŃł±¾Źż¾ŻµÄÖŠĪ»ŹżĀäŌŚµŚ¼ø×é£æ
£Ø3£©Čō²āŹŌ¾ÅÄź¼¶ÄŠÉś”°ÅÅĒņ30Ćė”±¶ŌĒ½µęĒņøöŹż²»µĶÓŚ10øöĪŖŗĻøń£¬øł¾ŻĶ³¼Ę½į¹ū£¬¹Ą¼ĘøĆŠ£¾ÅÄź¼¶450ĆūÄŠĶ¬Ń§³É¼ØŗĻøńµÄČĖŹż£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ![]() ”¢
Ӣ![]() Ӣ
”¢![]() ¶¼Óė
¶¼Óė![]() “¹Ö±£¬“¹×ć·Ö±šŹĒ
“¹Ö±£¬“¹×ć·Ö±šŹĒ![]() £¬
£¬![]() £¬
£¬![]() £¬ĒŅ
£¬ĒŅ![]() £¬
£¬![]() £¬ÄĒĆ“
£¬ÄĒĆ“![]() µÄ³¤£Ø £©
µÄ³¤£Ø £©
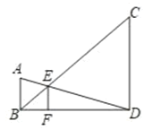
A.6B.9C.12D.16
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×”¢ŅŅ”¢±ū”¢¶”ĖÄĪ»Ķ¬Ń§½ųŠŠĘ¹ÅŅĒņµ„“ņ±ČČü£¬ŅŖ“ÓÖŠŃ”³öĮ½Ī»Ķ¬Ń§“ņµŚŅ»³”±ČČü£®
(1) ČōČ·¶Ø¼×“ņµŚŅ»³”£¬ŌŁ“ÓĘäӹȿĪ»Ķ¬Ń§ÖŠĖ껜єȔŅ»Ī»£¬Ē”ŗĆє֊ŅŅĶ¬Ń§µÄøÅĀŹŹĒ £®
(2) ČōĖ껜³éČ”Į½Ī»Ķ¬Ń§£¬ĒėÓĆ»Ź÷דĶ¼·Ø»ņĮŠ±ķ·Ø£¬ĒóĒ”ŗĆє֊¼×”¢ŅŅĮ½Ī»Ķ¬Ń§µÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
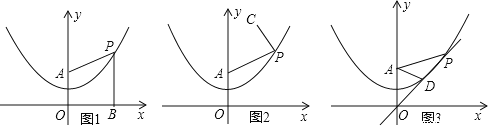
”¾ĢāÄæ”æŅŃÖŖ£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬µćAµÄ×ų±źĪŖ(0£¬2)£¬µćP(m£¬n)ŹĒÅ×ĪļĻß![]() ÉĻµÄŅ»øö¶Æµć.
ÉĻµÄŅ»øö¶Æµć.
(1)ČēĶ¼1£¬¹ż¶ÆµćP×÷PB”ĶxÖį£¬“¹×ćĪŖB£¬Į¬½ÓPA£¬ĒėĶعż²āĮæ»ņ¼ĘĖć£¬±Č½ĻPAÓėPBµÄ“󊔹ŲĻµ£ŗPA_____PB(Ö±½ÓĢīŠ“”°£¾”±”°£¼”±»ņ”°=”±£¬²»Šč½āĢā¹ż³Ģ)£»
(2)ĒėĄūÓĆ(1)µÄ½įĀŪ½ā¾öĻĀĮŠĪŹĢā£ŗ
¢ŁČēĶ¼2£¬ÉčCµÄ×ų±źĪŖ(2£¬5)£¬Į¬½ÓPC£¬AP+PCŹĒ·ń“ęŌŚ×īŠ”Öµ£æČē¹ū“ęŌŚ£¬ĒóµćPµÄ×ų±ź£»Čē¹ū²»“ęŌŚ£¬¼ņµ„ĖµĆ÷ĄķÓÉ£»
¢ŚČēĶ¼3£¬¹ż¶ÆµćPŗĶŌµćO×÷Ö±Ļß½»Å×ĪļĻßÓŚĮķŅ»µćD£¬ČōAP=2AD£¬ĒóÖ±ĻßOPµÄ½āĪöŹ½.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ä³Š£”°×ŪŗĻŹµ¼ł”±ÉēĶÅ£¬¼Ę»®ĄūÓĆ![]() ³¤µÄÕ¤Ąø²ÄĮĻ£¬Ņ»±ßææŌÓŠ¾ÉĒ½Ī§³ÉČēĶ¼ĖłŹ¾µÄĮ½øö¾ŲŠĪŹŌŃéĢļ£¬Ē½µÄ³¤¶ČĪŖ
³¤µÄÕ¤Ąø²ÄĮĻ£¬Ņ»±ßææŌÓŠ¾ÉĒ½Ī§³ÉČēĶ¼ĖłŹ¾µÄĮ½øö¾ŲŠĪŹŌŃéĢļ£¬Ē½µÄ³¤¶ČĪŖ![]() .
.
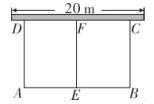
£Ø1£©ÄÜ·ńĪ§³É×ÜĆ껿ĪŖ![]() µÄŹŌŃéĢļ£æČōÄÜ£¬Ēó³ö
µÄŹŌŃéĢļ£æČōÄÜ£¬Ēó³ö![]() µÄ³¤¶Č£»Čō²»ÄÜ£¬ĖµĆ÷ĄķÓÉ£»
µÄ³¤¶Č£»Čō²»ÄÜ£¬ĖµĆ÷ĄķÓÉ£»
£Ø2£©ÄÜ·ńĪ§³É×ÜĆ껿ĪŖ![]() µÄŹŌŃéĢļ£æĖµĖµÄćµÄĄķÓÉ.
µÄŹŌŃéĢļ£æĖµĖµÄćµÄĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÅ×ĪļĻßy£½ax2+bx+c£Øa”Ł0£©µÄ¶Ō³ĘÖįĪŖx£½©1£¬ĒŅÅ×ĪļĻß¾¹ż A£Ø1£¬0£©£¬C£Ø0£¬3£©Į½µć£¬ÓėxÖį½»ÓŚµćB£®
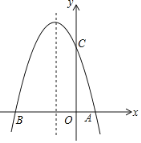
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ŌŚÅ×ĪļĻߵĶŌ³ĘÖįx£½©1ÉĻÕŅŅ»µćM£¬Ź¹µćMµ½µćAµÄ¾ąĄėÓėµ½µćCµÄ¾ąĄėÖ®ŗĶ×īŠ”£¬Ēó“ĖŹ±µćMµÄ×ų±ź£»
£Ø3£©ÉčµćPĪŖÅ×ĪļĻ߶Ō³ĘÖįx£½©1ÉĻµÄŅ»øö¶Æµć£¬ĒóŹ¹”÷BPCĪŖÖ±½ĒČż½ĒŠĪµÄµćPµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com