Question

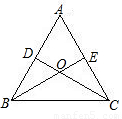
如图，等边△ABC中，点D、E分别是边AB、AC的中点，CD、BE交于点O，求∠BOC是多少度？

 

Answer 1

【答案】

120°

【解析】

试题分析：根据等边三角形的性质，确定CD、BE既为等边三角形的中线，又是三角形的高，然后根据四边形的内角和是360度解出∠DOE的度数，根据对顶角相等即可得出∠BOC的度数．

∵△ABC为等边三角形，点D、E分别是边AB、AC的中点；

∴∠ADC=∠BEA=90°；

∵在四边形ADOE中，∠A=60°，∠ADC=∠BEA=90°；

∴∠DOE=360°-60°-90°-90°=120°；

∵对顶角相等；

∴∠BOC=120°．

考点：此题考查了等边三角形的性质

点评：解答本题的关键是掌握等边三角形的“三线合一”： 底边上的高与底边上的中线，顶角的平分线重合。