
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则![]() 的度数为( )
的度数为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】D
【解析】
设∠ADE=x°,根据三角形外角性质,可得∠B+18°=x°+12°,可用x表示出∠B和∠C,再利用等腰三角形和外角的性质可表示出∠DAE和∠DEA,在△ADE中利用三角形内角和求得x,即可得∠DAE的度数.
解:设∠ADE=x°,
∵∠BAD=18°,∠EDC=12°,
∴∠B+18°=x°+12°,
∴∠B=x°-6°,
∵AB=AC,
∴∠C=∠B=x°-6°,
∴∠DEA=∠C+∠EDC=x°-6°+12°=x°+6°,
∵AD=DE,
∴∠DEA=∠DAE=x°+6°,
在△ADE中,由三角形内角和定理可得
x+x+6+x+6=180,
解得x=56,即∠ADE=56°,
∴∠DAE=62°
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() .
.![]() 分别是线段
分别是线段![]() ,
,![]() 上的点,连接
上的点,连接![]() ,使四边形
,使四边形![]() 为正方形,若点
为正方形,若点![]() 是
是![]() 上的动点,连接
上的动点,连接![]() ,将矩形沿
,将矩形沿![]() 折叠使得点
折叠使得点![]() 落在正方形
落在正方形![]() 的对角线所在的直线上,对应点为
的对角线所在的直线上,对应点为![]() ,则线段
,则线段![]() 的长为________.
的长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC、BD相交于点O,∠A=∠D,要使得△AOB≌△DOC,还需补充一个条件,下面补充的条件不一定正确的是( )
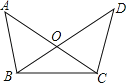
A.OA=ODB.AB=DCC.OB=OCD.∠ABO=∠DCO
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答问题:
分解因式:x3+3x2-4.
解答:把x=1代入多项式x3+3x2-4,发现此多项式的值为0,由此确定多项式x3+3x2-4中有因式(x-1),于是可设x3+3x2-4=(x-1)(x2+mx+n),分别求出m,n的值,再代入x3+3x2-4=(x-1)(x2+mx+n),就容易分解多项式x3+3x2-4.这种分解因式的方法叫“试根法”.
(1)求上述式子中m,n的值;
(2)请你用“试根法”分解因式:x3+x2-16x-16.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知 DE∥BC,CD 与 BE 相交于点 O,并且 S△DOE:S△COB=4:9,
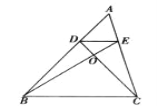
(1)求 AE:AC 的值;
(2)求△ADE 与四边形 DBCE 的面积比。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() ,
,![]() .
.
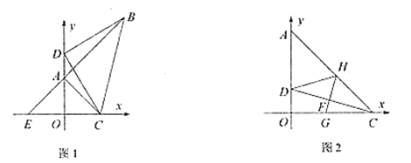
(1)若![]() ,
,![]() 满足
满足![]() .
.
①直接写出![]() ______,
______,![]() ______.
______.
②如图1,![]() 为点
为点![]() 上方一点,连接
上方一点,连接![]() ,在
,在![]() 轴右侧作等腰
轴右侧作等腰![]() ,
,![]() ,连接
,连接![]() 并延长交
并延长交![]() 轴于点
轴于点![]() ,当点
,当点![]() 上方运动时,求
上方运动时,求![]() 的面积;
的面积;
(2)如图2,若![]() ,点
,点![]() 在边
在边![]() 上,且
上,且![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 的垂线交
的垂线交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .连接
.连接![]() ,当
,当![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:AB⊥AC,DE⊥AB,AC=BE,BC=BD,

(1)求证:BC⊥BD;
(2)若点F是BC,BD的垂直平分线的交点,连接FA、FE.填空:判断△AFE的形状是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com