
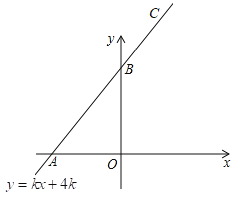
【题目】如图,一次函数![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且经过点
,且经过点![]() .
.
(1)当![]() 时;
时;
①求一次函数的表达式;
②![]() 平分
平分![]() 交
交![]() 轴于点
轴于点![]() ,求点
,求点![]() 的坐标;
的坐标;
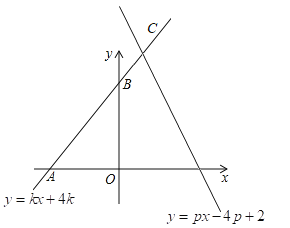
(2)若△![]() 为等腰三角形,求
为等腰三角形,求![]() 的值;
的值;
(3)若直线![]() 也经过点
也经过点![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)①![]() ;②(-
;②(-![]() ,0);(2)
,0);(2) ![]() ;(3)
;(3) ![]() .
.
【解析】
(1)①把x=2,y=![]() 代入
代入![]() 中求出k值即可;
中求出k值即可;
②作DE⊥AB于E,先求出点A、点B坐标,继而求出OA、OB、AB的长度,由角平分线的性质可得到OD=DE,于是BE=OB可求BE、AE的长,然后在![]() 中用勾股定理可列方程,解方程即可求得OD的长;
中用勾股定理可列方程,解方程即可求得OD的长;
(2)求得点A坐标是(-4,0),点C坐标是(2,![]() ),由△
),由△![]() 为等腰三角形,可知OC=OA=4,故
为等腰三角形,可知OC=OA=4,故![]() ,解方程即可;
,解方程即可;
(3) 由直线![]() 经过点
经过点![]()
![]() , 得
, 得![]() =
=![]() ,由(2)知
,由(2)知![]() ,故
,故![]() ,用k表示p代入
,用k表示p代入![]() 中得到关于k的不等式,解不等式即可.
中得到关于k的不等式,解不等式即可.
解:(1)当![]() 时,点C坐标是
时,点C坐标是![]() ,
,
①把x=2,y=![]() 代入
代入![]() 中,
中,
得![]() ,
,
解得![]() ,
,
所以一次函数的表达式是![]() ;
;
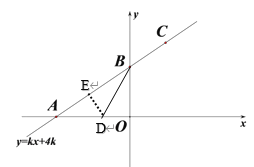
②如图,![]() 平分
平分![]() 交
交![]() 轴于点
轴于点![]() ,作DE⊥AB于E,
,作DE⊥AB于E,
∵在![]() 中,当x=0时,y=3;当y=0时,x=-4,
中,当x=0时,y=3;当y=0时,x=-4,
∴点A坐标是(-4,0),点B坐标是(0,3),
∴OA=4,OB=3,
∴![]() ,
,
∵![]() 平分
平分![]() , DE⊥AB, DO⊥OB,
, DE⊥AB, DO⊥OB,
∴OD=DE,
∵BD=BD,
∴![]() ,
,
∴BE=OB=3,
∴AE=AB-BE=5-3=2,
∵在![]() 中,
中,![]() ,
,
∴![]() ,
,
∴OD= ![]() ,
,
∴点D坐标是(-![]() ,0),
,0),
(2) ∵在![]() 中,当y=0时,x=-4;当x=2时,y=
中,当y=0时,x=-4;当x=2时,y=![]() ,
,
∴点A坐标是(-4,0),点C坐标是(2,![]() ),
),
∵△![]() 为等腰三角形,
为等腰三角形,
∴OC=OA=4,
∴![]() ,
,
∴![]() ,
,![]() (不合题意,舍去),
(不合题意,舍去),
∴![]() .
.
(3) ∵直线![]() 经过点
经过点![]()
![]() ,
,
∴![]() =
=![]() ,
,
由(2)知![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:
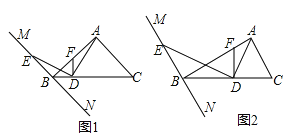
【题目】在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.
(1)如图①,当∠ABC=45°时,求证:AD=DE;理由;
(2)如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;
(3)当∠ABC=α时,请直接写出线段AD与DE的数量关系.(用含α的三角函数表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
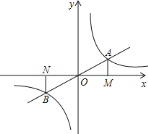
【题目】如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 在第一象限的图象交于
在第一象限的图象交于![]() 点,过
点,过![]() 点作
点作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,已知
,已知![]() 的面积为
的面积为![]() .
.
![]() 求反比例函数的解析式;
求反比例函数的解析式;
![]() 如图,点
如图,点![]() 为反比例函数在第三象限图象上的点,过
为反比例函数在第三象限图象上的点,过![]() 点作
点作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年11月20日-23日,首届世界![]() 大会在北京举行.某校的学生开展对于
大会在北京举行.某校的学生开展对于![]() 知晓情况的问卷调查,问卷调查的结果分为
知晓情况的问卷调查,问卷调查的结果分为![]() 、
、![]() 、
、![]() 、
、![]() 四类,其中
四类,其中![]() 类表示“非常了解”,
类表示“非常了解”,![]() 类表示“比较了解”,
类表示“比较了解”,![]() 类表示“基本了解”,
类表示“基本了解”,![]() 类表示“不太了解”,并把调查结果绘制成如图所示的两个统计图表(不完整).
类表示“不太了解”,并把调查结果绘制成如图所示的两个统计图表(不完整).
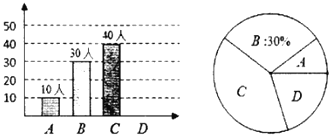
根据上述信息,解答下列问题:
(1)这次一共调查了多少人;
(2)求“![]() 类”在扇形统计图中所占圆心角的度数;
类”在扇形统计图中所占圆心角的度数;
(3)请将条形统计图补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() ,过顶点
,过顶点![]() 作射线
作射线![]() .
.
(1)当射线![]() 在
在![]() 外部时,如图①,点
外部时,如图①,点![]() 在射线
在射线![]() 上,连结
上,连结![]() 、
、![]() ,已知
,已知![]() ,
,![]() ,
,![]() (
(![]() ).
).
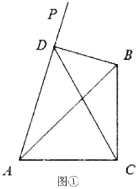
①试证明![]() 是直角三角形;
是直角三角形;
②求线段![]() 的长.(用含
的长.(用含![]() 的代数式表示)
的代数式表示)
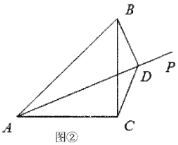
(2)当射线![]() 在
在![]() 内部时,如图②,过点
内部时,如图②,过点![]() 作
作![]() 于点
于点![]() ,连结
,连结![]() ,请写出线段
,请写出线段![]() 、
、![]() 、
、![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
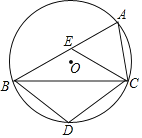
【题目】如图,△ABC是⊙O的内接三角形,点D在![]() 上,点E在弦AB上(E不与A重合),且四边形BDCE为菱形.
上,点E在弦AB上(E不与A重合),且四边形BDCE为菱形.
(1)求证:AC=CE;
(2)求证:BC2﹣AC2=ABAC;
(3)已知⊙O的半径为3.
①若![]() =
=![]() ,求BC的长;
,求BC的长;
②当![]() 为何值时,ABAC的值最大?
为何值时,ABAC的值最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一次函数![]() (
(![]() 为常数)的图像位于
为常数)的图像位于![]() 轴下方的部分沿
轴下方的部分沿![]() 轴翻折到
轴翻折到![]() 轴上方,和一次函数
轴上方,和一次函数![]() (
(![]() 为常数)的图像位于
为常数)的图像位于![]() 轴及上方的部分组成“
轴及上方的部分组成“![]() ”型折线,过点
”型折线,过点![]() 作
作![]() 轴的平行线
轴的平行线![]() ,若该“
,若该“![]() ”型折线在直线
”型折线在直线![]() 下方的点的横坐标
下方的点的横坐标![]() 满足
满足![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com