
如图,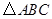 中,
中,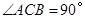 ,将
,将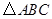 沿着一条直线折叠后,使点
沿着一条直线折叠后,使点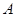 与点
与点 重合(图②).
重合(图②).
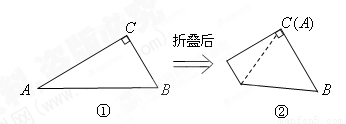
(1)在图①中画出折痕所在的直线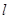 .设直线
.设直线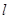 与
与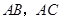 分别相交于点
分别相交于点 ,连结
,连结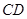 .(尺规作图,保留作图痕迹,不要求写画法)(2分)
.(尺规作图,保留作图痕迹,不要求写画法)(2分)
(2)请你找出完成问题(1)后所得到的图形中的等腰三角形.(用字母表示,不要求证明)(2分)
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012年初中毕业升学考试(山西卷)数学(带解析) 题型:解答题
问题情境:将一副直角三角板(Rt△ABC和Rt△DEF)按图1所示的方式摆放,其中∠ACB=90°,CA=CB,∠FDE=90°,O是AB的中点,点D与点O重合,DF⊥AC于点M,DE⊥BC于点N,试判断线段OM与ON的数量关系,并说明理由.
探究展示:小宇同学展示出如下正确的解法:
解:OM=ON,证明如下:
连接CO,则CO是AB边上中线,
∵CA=CB,∴CO是∠ACB的角平分线.(依据1)
∵OM⊥AC,ON⊥BC,∴OM=ON.(依据2)
反思交流:
(1)上述证明过程中的“依据1”和“依据2”分别是指:
依据1:
依据2:
(2)你有与小宇不同的思考方法吗?请写出你的证明过程.
拓展延伸:
(3)将图1中的Rt△DEF沿着射线BA的方向平移至如图2所示的位置,使点D落在BA的延长线上,FD的延长线与CA的延长线垂直相交于点M,BC的延长线与DE垂直相交于点N,连接OM、ON,试判断线段OM、ON的数量关系与位置关系,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年云南省玉溪市洛河民族中学八年级上期末考试数学卷(带解析) 题型:解答题
如图,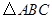 中,
中,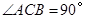 ,将
,将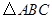 沿着一条直线折叠后,使点
沿着一条直线折叠后,使点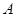 与点
与点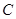 重合(图②).
重合(图②).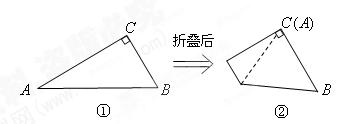
(1)在图①中画出折痕所在的直线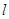 .设直线
.设直线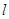 与
与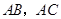 分别相交于点
分别相交于点 ,连结
,连结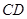 .(尺规作图,保留作图痕迹,不要求写画法)(2分)
.(尺规作图,保留作图痕迹,不要求写画法)(2分)
(2)请你找出完成问题(1)后所得到的图形中的等腰三角形.(用字母表示,不要求证明)(2分)
查看答案和解析>>
科目:初中数学 来源:山西省中考真题 题型:解答题
 B的中点,点D与点O重合,DF⊥AC于点M,DE⊥BC于点N,试判断线段OM与ON的数量关系,并说明理由
B的中点,点D与点O重合,DF⊥AC于点M,DE⊥BC于点N,试判断线段OM与ON的数量关系,并说明理由
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com