
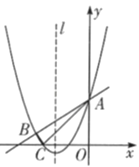
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþy£Ω![]() x2+bx+c”Î÷±œþy£Ω
x2+bx+c”Î÷±œþy£Ω![]() x+3∑÷±œýΩª”⁄A£¨B¡Ωµ„£¨«“¥À≈◊ŒÔœþ”Îx÷·µƒ“ª∏ˆΩªµ„Œ™C£¨¡¨Ω”AC£¨BC£Æ“—÷™A£®0£¨3£©£¨C£®©Å3£¨0£©£Æ
x+3∑÷±œýΩª”⁄A£¨B¡Ωµ„£¨«“¥À≈◊ŒÔœþ”Îx÷·µƒ“ª∏ˆΩªµ„Œ™C£¨¡¨Ω”AC£¨BC£Æ“—÷™A£®0£¨3£©£¨C£®©Å3£¨0£©£Æ
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©‘⁄≈◊ŒÔœþ∂‘≥∆÷·l…œ’““ªµ„M£¨ π|MB©ÅMC|µƒ÷µ◊Ó¥Û£¨≤¢«Û≥ˆ’‚∏ˆ◊Ó¥Û÷µ£ª
£®3£©µ„PŒ™y÷·”“≤ý≈◊ŒÔœþ…œ“ª∂ص„£¨¡¨Ω”PA£¨π˝µ„P◊˜PQ°ÕPAΩªy÷·”⁄µ„Q£¨Œ £∫ «∑ҥʑ⁄µ„P πµ√“‘A£¨P£¨QŒ™∂•µ„µƒ»˝Ω«–Œ”ΰ˜ABCœýÀ∆£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆÀ˘”–∑˚∫œÃıº˛µƒµ„Pµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©y£Ω![]() x2+
x2+![]() x+3£ª£®2£©|MB©ÅMC|»°◊Ó¥Û÷µŒ™
x+3£ª£®2£©|MB©ÅMC|»°◊Ó¥Û÷µŒ™![]() £ª£®3£©¥Ê‘⁄£¨µ„P£®1£¨6£©£Æ
£ª£®3£©¥Ê‘⁄£¨µ„P£®1£¨6£©£Æ
°æΩ‚Œˆ°ø
£®1£©¢ŸΩ´A£®0£¨3£©£¨C£®-3£¨0£©¥˙»Îy=![]() x2+bx+c£¨º¥ø…«ÛΩ‚£ª
x2+bx+c£¨º¥ø…«ÛΩ‚£ª
£®2£©∑÷µ±µ„B°¢C°¢M»˝µ„≤ªπ≤œþ ±°¢µ±µ„B°¢C°¢M»˝µ„π≤œþ ±£¨¡Ω÷÷«Èøˆ∑÷±«ÛΩ‚º¥ø…£ª
£®3£©∑÷µ±![]() ±°¢µ±
±°¢µ±![]() ±¡Ω÷÷«Èøˆ£¨∑÷±«ÛΩ‚º¥ø…£Æ
±¡Ω÷÷«Èøˆ£¨∑÷±«ÛΩ‚º¥ø…£Æ
£®1£©Ω´A£®0£¨3£©£¨C£®©Å3£¨0£©¥˙»Îy£Ω![]() x2+bx+c£¨
x2+bx+c£¨
µ√ £¨
£¨
Ω‚µ√![]() £¨
£¨
°ý≈◊ŒÔœþµƒΩ‚Œˆ Ω «y£Ω![]() x2+
x2+![]() x+3£ª
x+3£ª
£®2£©Ω´÷±œþy£Ω![]() x+3±Ì¥Ô Ω”Î∂˛¥Œ∫Ø ˝±Ì¥Ô Ω¡™¡¢≤¢Ω‚µ√£∫x£Ω0ªÚ©Å4£¨
x+3±Ì¥Ô Ω”Î∂˛¥Œ∫Ø ˝±Ì¥Ô Ω¡™¡¢≤¢Ω‚µ√£∫x£Ω0ªÚ©Å4£¨
°þA £®0£¨3£©£¨
°ýB£®©Å4£¨1£©
¢Ÿµ±µ„B°¢C°¢M»˝µ„≤ªπ≤œþ ±£¨
|MB©ÅMC|£ºBC£¨
¢⁄µ±µ„B°¢C°¢M»˝µ„π≤œþ ±£¨
|MB©ÅMC|£ΩBC£¨
°ýµ±µ„°¢C°¢M»˝µ„π≤œþ ±£¨|MB©ÅMC|»°◊Ó¥Û÷µ£¨º¥Œ™BCµƒ≥§£¨
π˝µ„B◊˜x÷·”⁄µ„E£¨

‘⁄Rt°˜BEC÷–£¨”…π¥π…∂®¿Ìµ√BC£Ω![]() £Ω
£Ω![]() £¨
£¨
°ý|MB©ÅMC|»°◊Ó¥Û÷µŒ™![]() £ª
£ª
£®3£©¥Ê‘⁄µ„P πµ√“‘A°¢P°¢QŒ™∂•µ„µƒ»˝Ω«–Œ”ΰ˜ABCœýÀ∆£Æ
…˵„P◊¯±ÍŒ™£®x£¨![]() x2+
x2+![]() x+3£©£®x£æ0£©
x+3£©£®x£æ0£©
‘⁄Rt°˜BEC÷–£¨
°þBE£ΩCE£Ω1£¨
°ý°œBCE£Ω45°„£¨
‘⁄Rt°˜ACO÷–£¨
°þAO£ΩCO£Ω3£¨
°ý°œACO£Ω45°„£¨
°ý°œACB£Ω180°„©Å450©Å450£Ω900£¨AC£Ω3![]() £¨
£¨
π˝µ„P◊˜PQ°ÕPA”⁄µ„P£¨‘Ú°œAPQ£Ω90°„£¨π˝µ„P◊˜PQ°Õy÷·”⁄µ„G£¨

°þ°œPQA£Ω°œAPQ£Ω90°„
°œPAG£Ω°œQAP£¨
°ý°˜PGA°◊°˜QPA
°þ°œPGA£Ω°œACB£Ω90°„
°ý¢Ÿµ±![]() ±£¨
±£¨
°˜PAG°◊°˜BAC£¨
°ý £¨
£¨
Ω‚µ√x1£Ω1£¨x2£Ω0£¨£®…·»•£©
°ýµ„Pµƒ◊ð◊¯±ÍŒ™![]() °¡12+
°¡12+![]() °¡1+3£Ω6£¨
°¡1+3£Ω6£¨
°ýµ„PŒ™£®1£¨6£©£ª
¢⁄µ±![]() ±£¨
±£¨
°˜PAG°◊°˜ABC£¨
°ý £¨
£¨
Ω‚µ√x1£Ω©Å![]() £®…·»•£©£¨x2£Ω0£®…·»•£©£¨
£®…·»•£©£¨x2£Ω0£®…·»•£©£¨
°ý¥À ±ŒÞ∑˚∫œÃıº˛µƒµ„P
◊€…œÀ˘ ˆ£¨¥Ê‘⁄µ„P£®1£¨6£©£Æ


 √˚–£øŒÃ√œµ¡–¥∞∏
√˚–£øŒÃ√œµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
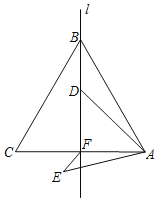
°æƒø°ø»ÁÕº£¨µ»±þ»˝Ω«–Œ°˜ABCµƒ±þ≥§Œ™6£¨l «AC±þ…œµƒ∏þBFÀ˘‘⁄µƒ÷±œþ£¨µ„DŒ™÷±œþl…œµƒ“ª∂ص„£¨¡¨Ω”AD£¨≤¢Ω´AD»∆µ„AƒÊ ±’Ζ˝◊™60°„÷¡AE£¨¡¨Ω”EF£¨‘ÚEFµƒ◊Ó–°÷µŒ™_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
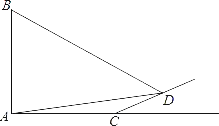
°æƒø°ø»ÁÕº£¨∆Ï∏ÀABµƒ∂•∂ÀB‘⁄œ¶—Ùµƒ”ýª‘œ¬¬‰‘⁄“ª∏ˆ–±∆¬…œµƒµ„D¥¶£¨ƒ≥–£ ˝—ßøŒÕ‚–À»§–°◊ȵƒÕ¨—ß’˝‘⁄≤‚¡ø∆Ï∏Àµƒ∏þ∂»£¨‘⁄∆Ï∏Àµƒµ◊≤øA¥¶≤‚µ√µ„Dµƒ—ˆΩ«Œ™15°„£¨AC£Ω10√◊£¨”÷≤‚µ√°œBDA£Ω45°„£Æ“—÷™–±∆¬CDµƒ∆¬∂»Œ™i£Ω1£∫![]() £¨«Û∆Ï∏ÀABµƒ∏þ∂»£®
£¨«Û∆Ï∏ÀABµƒ∏þ∂»£®![]() £¨Ω·π˚æ´»∑µΩ∏ˆŒª£©£Æ
£¨Ω·π˚æ´»∑µΩ∏ˆŒª£©£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥∞ýŒ™≤Œº”—ß–£µƒ¥ÛøŒº‰ªÓ∂ر»»¸£¨◊º±∏π∫Ω¯“ª≈˙ï…˛£¨“—÷™2∏˘![]() –Õï…˛∫Õ1∏˘
–Õï…˛∫Õ1∏˘![]() –Õï…˛π≤–Ë56‘™£¨1∏˘
–Õï…˛π≤–Ë56‘™£¨1∏˘![]() –Õï…˛∫Õ2∏˘
–Õï…˛∫Õ2∏˘![]() –Õï…˛π≤–Ë82‘™£Æ
–Õï…˛π≤–Ë82‘™£Æ
£®1£©«Û“ª∏˘![]() –Õï…˛∫Õ“ª∏˘
–Õï…˛∫Õ“ª∏˘![]() –Õï…˛µƒ €º€∏˜ «∂ý…Ÿ‘™£ø
–Õï…˛µƒ €º€∏˜ «∂ý…Ÿ‘™£ø
£®2£©—ß–£◊º±∏π∫Ω¯’‚¡Ω÷÷–Õ∫≈µƒÃ¯…˛π≤50∏˘£¨≤¢«“![]() –Õï…˛µƒ ˝¡ø≤ª∂ý”⁄
–Õï…˛µƒ ˝¡ø≤ª∂ý”⁄![]() –Õï…˛ ˝¡øµƒ3±∂£¨«Î…˺∆≥ˆ◊Ó °«Æµƒπ∫¬Ú∑Ω∞∏£¨≤¢Àµ√˜¿Ì”…£Æ
–Õï…˛ ˝¡øµƒ3±∂£¨«Î…˺∆≥ˆ◊Ó °«Æµƒπ∫¬Ú∑Ω∞∏£¨≤¢Àµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∆Î∆Îπ˛∂˚ –ΩÔ˝æ÷œÎ÷™µ¿ƒ≥–£—ß…˙∂‘‘˙¡˙◊‘»ª±£ª§«¯µƒ¡ÀΩ‚≥Ã∂»£¨‘⁄∏√–£Àʪ˙≥È»°¡À≤ø∑÷—ß…˙Ω¯––Œ æÌ£¨Œ æÌ”–“‘œ¬Àƒ∏ˆ—°œÓ£∫A£Æ Æ∑÷¡ÀΩ‚£ªB£Æ¡ÀΩ‚Ωœ∂ý£∫C£Æ¡ÀΩ‚Ωœ…Ÿ£∫D£Æ≤ª¡ÀΩ‚£®“™«Û£∫√ø√˚±ªµ˜≤ȵƒ—ß…˙±ÿ—°«“÷ªƒÐ—°‘Ò“ªœÓ£©£Æœ÷Ω´µ˜≤ȵƒΩ·π˚ªÊ÷∆≥…¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº£Æ«Î∏˘æð¡Ω∑˘Õ≥º∆Õº÷–µƒ–≈œ¢ªÿ¥œ¬¡–Œ £∫
£®1£©±æ¥Œ±ª≥È»°µƒ—ß…˙π≤”–_______√˚£ª
£®2£©«Î≤π»´Ãı–ŒÕº£ª
£®3£©…»–ŒÕº÷–µƒ—°œÓ°∞C£Æ¡ÀΩ‚Ωœ…Ÿ°±≤ø∑÷À˘’º…»–Œµƒ‘≤–ƒΩ«µƒ¥Û–°Œ™_______°„£ª
£®4£©»Ù∏√–£π≤”–![]() √˚—ß…˙£¨«Îƒ„∏˘æð…œ ˆµ˜≤ÈΩ·π˚π¿º∆∏√–£∂‘”⁄‘˙¡˙◊‘»ª±£ª§«¯°∞ Æ∑÷¡ÀΩ‚°±∫Õ°∞¡ÀΩ‚Ωœ∂ý°±µƒ—ß…˙π≤”–∂ý…Ÿ√˚£ø
√˚—ß…˙£¨«Îƒ„∏˘æð…œ ˆµ˜≤ÈΩ·π˚π¿º∆∏√–£∂‘”⁄‘˙¡˙◊‘»ª±£ª§«¯°∞ Æ∑÷¡ÀΩ‚°±∫Õ°∞¡ÀΩ‚Ωœ∂ý°±µƒ—ß…˙π≤”–∂ý…Ÿ√˚£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº1£¨‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨∞Îæ∂Œ™1µƒ°—O”Îx÷·’˝∞Î÷·∫Õy÷·’˝∞Î÷·∑÷±Ωª”⁄A£¨B¡Ωµ„£¨÷±œþl£∫y£Ωkx+2£®k£º0£©”Îx÷·∫Õy÷·∑÷±Ωª”⁄P£¨M¡Ωµ„£Æ
£®1£©µ±÷±œþ”ΰ—Oœý«– ±£¨«Û≥ˆµ„Mµƒ◊¯±Í∫Õµ„Pµƒ◊¯±Í£ª
£®2£©»ÁÕº2£¨µ±µ„P‘⁄œþ∂ŒOA…œ ±£¨÷±œþ1”ΰ—OΩª”⁄E£¨F¡Ωµ„£®µ„E‘⁄µ„Fµƒ…œ∑Ω£©π˝µ„F◊˜FC°Œx÷·£¨”ΰ—OΩª”⁄¡Ì“ªµ„C£¨¡¨Ω·ECΩªy÷·”⁄µ„D£Æ
¢Ÿ»ÁÕº3£¨»Ùµ„P”ε„A÷ÿ∫œ ±£¨«ÛODµƒ≥§≤¢–¥≥ˆΩ‚¥π˝≥ãª
¢⁄»ÁÕº2£¨»Ùµ„P”ε„A≤ª÷ÿ∫œ ±£¨ODµƒ≥§ «∑Ò∑¢…˙±‰ªØ£¨»Ù≤ª∑¢…˙±‰ªØ£¨«Î«Û≥ˆODµƒ≥§≤¢–¥≥ˆΩ‚¥π˝≥㪻Ù∑¢…˙±‰ªØ£¨«ÎÀµ√˜¿Ì”…£Æ
£®3£©»ÁÕº4£¨‘⁄£®2£©µƒª˘¥°…œ£¨¡¨Ω·BF£¨Ω´œþ∂ŒBF»∆µ„BƒÊ ±’Ζ˝◊™90°„µΩBQ£¨»Ùµ„Q‘⁄CEµƒ—”≥§œþ ±£¨«Î”√µ» Ω÷±Ω”±Ì æœþ∂ŒFC£¨FQ÷ƺ‰µƒ ˝¡øπÿœµ£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø—ß–£÷≤ŒÔ‘∞—ÿ¬∑ª§¿∏µƒŒ∆ Œ≤ø∑÷…˺∆≥…»Ù∏…∏ˆ»´µ»¡‚–ŒÕº∞∏£¨√ø‘ˆº”“ª∏ˆ¡‚–ŒÕº∞∏£¨Œ∆ Œ≥§∂»æÕ‘ˆº”dcm£¨»ÁÕºÀ˘ 棨“—÷™√ø∏ˆ¡‚–ŒÕº∞∏µƒ±þ≥§Œ™10![]() cm£¨∆‰÷–“ª∏ˆƒ⁄Ω«Œ™60°„£Æ
cm£¨∆‰÷–“ª∏ˆƒ⁄Ω«Œ™60°„£Æ
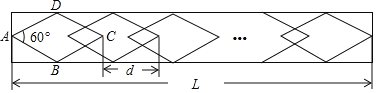
(1)«Û“ª∏ˆ¡‚–ŒÕº∞∏ÀÆ∆Ω∑ΩœÚµƒ∂‘Ω«œþ≥§£ª
(2)»Ùd£Ω26£¨Œ∆ Œµƒ≥§∂»LƒÐ∑Ò «6010cm£ø»ÙƒÐ£¨«Û≥ˆ¡‚–Œ∏ˆ ˝£ª»Ù≤ªƒÐ£¨Àµ√˜¿Ì”…£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øΩ´¡ΩøÈ÷±Ω«»˝Ω«∞»ÁÕº1∑≈÷√£¨µ»—¸÷±Ω«»˝Ω«∞Â![]() µƒ÷±Ω«∂•µ„ «µ„
µƒ÷±Ω«∂•µ„ «µ„![]() £¨
£¨![]() £¨÷±Ω«∞Â
£¨÷±Ω«∞Â![]() µƒ÷±Ω«∂•µ„
µƒ÷±Ω«∂•µ„![]() ‘⁄
‘⁄![]() …œ£¨«“
…œ£¨«“![]() £¨
£¨![]() £Æ»˝Ω«∞Â
£Æ»˝Ω«∞Â![]() πÃ∂®≤ª∂Ø£¨Ω´»˝Ω«∞Â
πÃ∂®≤ª∂Ø£¨Ω´»˝Ω«∞Â![]() »∆µ„
»∆µ„![]() ƒÊ ±’Ζ˝◊™£¨–˝◊™Ω«Œ™
ƒÊ ±’Ζ˝◊™£¨–˝◊™Ω«Œ™![]()
![]() £Æ
£Æ
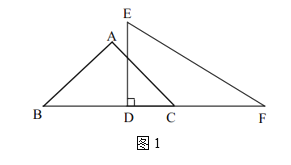
£®1£©µ±![]() _______ ±£¨
_______ ±£¨![]() £ª
£ª
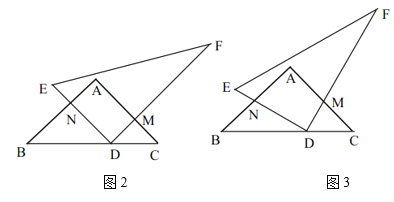
£®2£©µ±![]() ±£¨»˝Ω«∞Â
±£¨»˝Ω«∞Â![]() »∆µ„
»∆µ„![]() ƒÊ ±’Ζ˝◊™÷¡»ÁÕº2Œª÷√£¨…Ë
ƒÊ ±’Ζ˝◊™÷¡»ÁÕº2Œª÷√£¨…Ë![]() ”Î
”Î![]() Ωª”⁄µ„
Ωª”⁄µ„![]() £¨
£¨![]() Ωª
Ωª![]() ”⁄µ„
”⁄µ„![]() £¨«ÛÀƒ±þ–Œ
£¨«ÛÀƒ±þ–Œ![]() µƒ√ʪ˝£Æ
µƒ√ʪ˝£Æ
£®3£©»ÁÕº3£¨…Ë![]() £¨Àƒ±þ–Œ
£¨Àƒ±þ–Œ![]() µƒ√ʪ˝Œ™
µƒ√ʪ˝Œ™![]() £¨«Û
£¨«Û![]() πÿ”⁄
πÿ”⁄![]() µƒ±Ì¥Ô Ω£®≤ª”√–¥
µƒ±Ì¥Ô Ω£®≤ª”√–¥![]() µƒ»°÷µ∑∂Œß£©£Æ
µƒ»°÷µ∑∂Œß£©£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
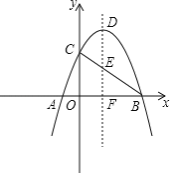
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþ![]() ”Îx÷·œýΩª”⁄A°¢B¡Ωµ„£¨”Îy÷·Ωª”⁄C£¨∂•µ„Œ™D£¨≈◊ŒÔœþµƒ∂‘≥∆÷·DF”ÎBCœýΩª”⁄µ„E£¨”Îx÷·œýΩª”⁄µ„F£Æ
”Îx÷·œýΩª”⁄A°¢B¡Ωµ„£¨”Îy÷·Ωª”⁄C£¨∂•µ„Œ™D£¨≈◊ŒÔœþµƒ∂‘≥∆÷·DF”ÎBCœýΩª”⁄µ„E£¨”Îx÷·œýΩª”⁄µ„F£Æ
£®1£©«Ûœþ∂ŒDEµƒ≥§£ª
£®2£©…Ëπ˝Eµƒ÷±œþ”Î≈◊ŒÔœþœýΩª”⁄M(x1£¨y1)£¨N(x2£¨y2)£¨ ‘≈–∂œµ±|x1©Åx2|µƒ÷µ◊Ó–° ±£¨÷±œþMN”Îx÷·µƒŒª÷√πÿœµ£¨≤¢Àµ√˜¿Ì”…£ª
£®3£©…ËPŒ™x÷·…œµƒ“ªµ„£¨°œDAO+°œDPO=°œ¶¡£¨µ±tan°œ¶¡=4 ±£¨«Ûµ„Pµƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com