
����Ŀ����1�����ⷢ��
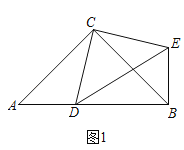
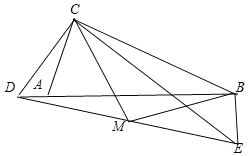
��ͼ1����Rt��ABC��Rt��CDE�У���ACB����DCE��90������CAB����CDE��45������Dʱ�߶�AB��һ���㣬����BE��
��գ���![]() ��ֵΪ�� ���� �ڡ�DBE�Ķ���Ϊ�� ����
��ֵΪ�� ���� �ڡ�DBE�Ķ���Ϊ�� ����
��2�����̽��
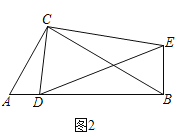
��ͼ2����Rt��ABC��Rt��CDE�У���ACB����DCE��90������CAB����CDE��60������D���߶�AB��һ���㣬����BE�����ж�![]() ��ֵ����DBE�Ķ�������˵�����ɣ�
��ֵ����DBE�Ķ�������˵�����ɣ�
��3����չ����
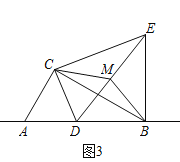
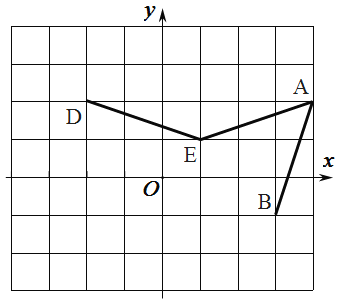
��ͼ3���ڣ�2���������£�����D��Ϊֱ��AB��һ���㣬�����������䣬ȡ�߶�DE���е�M������BM��CM����AC��2������CBM��ֱ��������ʱ���߶�BE�ij��Ƕ��٣���ֱ��д���𰸣�
���𰸡���1����1�� ��90������2��![]() ��
��![]() ����DBE��90�������ɼ���������3��BE�ij�Ϊ3+
����DBE��90�������ɼ���������3��BE�ij�Ϊ3+![]() ��3��
��3��![]()
��������
��1����ֱ�������ε����ʿɵá�ABC��45�����ɵá�DBE��90����ͨ��֤����ACD�ס�BCE���ɵ�![]() ��ֵ��
��ֵ��
��2��ͨ��֤����ACD�ס�BCE���ɵ�![]() ��ֵ����CBE����CAD��60�����������DBE�Ķ�����
��ֵ����CBE����CAD��60�����������DBE�Ķ�����
��3���ֵ�D���߶�AB�Ϻ�BA�ӳ���������������ۣ���ֱ�������ε����ʿ�֤CM��BM��![]() ��������DE��2
��������DE��2![]() �������������ε����ʿɵá�ABE��90����BE��
�������������ε����ʿɵá�ABE��90����BE��![]() AD���ɹ��ɶ�������BE�ij���
AD���ɹ��ɶ�������BE�ij���
�⣺��1���ߡ�ACB��90������CAB��45����
���ABC����CAB��45����
��AC��BC����DBE����ABC+��CBE��90����
�ߡ�ACB����DCE��90����
���ACD����BCE���ҡ�CAB����CDE��45����
���ACD�ס�BCE��
��![]() ��
��
�ʴ�Ϊ��1��90����
��2��![]() ����DBE��90����
����DBE��90����
���ɣ��ߡ�ACB����DCE��90������CAB����CDE��60����
���ACD����BCE����CED����ABC��30����
��tan��ABC��tan30����![]() ��
��![]() ��
��
�ߡ�ACB����DCE��90������CAB����CDE��60����
��Rt��ACB��Rt��DCE��
��![]() ��
��
��![]() ���ҡ�ACD����BCE��
���ҡ�ACD����BCE��
���ACD�ס�BCE��
��![]() ��
��![]() ����CBE����CAD��60����
����CBE����CAD��60����
���DBE����ABC+��CBE��90����
��3������D���߶�AB�ϣ���ͼ��
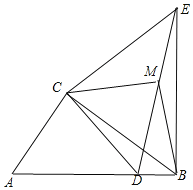
�ɣ�2��֪��![]() ��
��![]() ����ABE��90����
����ABE��90����
��BE��![]() AD��
AD��
��AC��2����ACB��90������CAB��90����
��AB��4��BC��2![]() ��
��
�ߡ�ECD����ABE��90�����ҵ�M��DE�е㣬
��CM��BM��![]() DE��
DE��
����CBM��ֱ�������Σ�
��CM2+BM2��BC2����2![]() ��2��
��2��
��BM��CM��![]() ��
��
��DE��2![]() ��
��
��DB2+BE2��DE2��
�ࣨ4��AD��2+��![]() AD��2��24��
AD��2��24��
��AD��![]() +1��
+1��
��BE��![]() AD��3+
AD��3+![]() ��
��
����D���߶�BA�ӳ����ϣ���ͼ��
ͬ���ɵã�DE��2![]() ��BE��
��BE��![]() AD��
AD��
��BD2+BE2��DE2��
�ࣨ4+AD��2+��![]() AD��2��24��
AD��2��24��
��AD��![]() ��1��
��1��
��BE��![]() AD��3��
AD��3��![]() ��
��
����������BE�ij�Ϊ3+![]() ��3��
��3��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() �Ķ�������Ϊ
�Ķ�������Ϊ![]() ��
��![]() .
.
��1�����ú���ͼ�����![]() .
.
����ú�������ʽ��
��![]() ������ͼ���ϵ�
������ͼ���ϵ�![]() ��x��ľ�����СֵΪ1����t��ֵΪ______��
��x��ľ�����СֵΪ1����t��ֵΪ______��
��2������P�ں���![]() ��ͼ���ϣ���
��ͼ���ϣ���![]() ����h�����ֵ.
����h�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
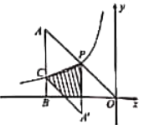
����Ŀ����ͼ��PΪ˫����![]() ��һ����.����OP���ӳ�����A��ʹ
��һ����.����OP���ӳ�����A��ʹ![]() ������A��x��Ĵ��ߣ�����ΪB����˫�����ڵ�C.��
������A��x��Ĵ��ߣ�����ΪB����˫�����ڵ�C.��![]() ʱ������PC����
ʱ������PC����![]() ��ֱ��PC���з��ۣ����ۺ��
��ֱ��PC���з��ۣ����ۺ��![]() ���ı���BOPC���ص����֣�ͼ����Ӱ���֣��������_______________
���ı���BOPC���ص����֣�ͼ����Ӱ���֣��������_______________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
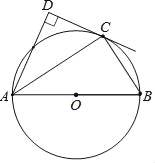
����Ŀ����ͼ����C����ABΪֱ������O�ϣ�AD�����C�����ߴ�ֱ������Ϊ��D��
��1����֤��ACƽ����DAB��
��2����֤��AC2=ADAB��
��3����AD=![]() ��sinB=
��sinB=![]() �����߶�BC�ij���
�����߶�BC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���B=90������BAC��ƽ���߽�BC�ڵ�D����DΪԲ�ģ�D��Ϊ�뾶������D.
����֤��AC�ǡ�D������.
����AC���D���ڵ�E��DB=1������DE��BF��EF.
�ٵ���BAD= ʱ���ı���BDEFΪ���Σ�
�ڵ�AB= ʱ����CDEΪ����������.
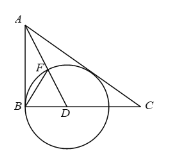
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ��
��![]() ��P��BC��һ���㣬��P��AP�Ĵ��߽�CD��E����
��P��BC��һ���㣬��P��AP�Ĵ��߽�CD��E����![]() ���۵õ�
���۵õ�![]() ���ӳ�FP��AB��H������AE��PE��AC��G.
���ӳ�FP��AB��H������AE��PE��AC��G.

��1����֤![]() ��
��
��2����![]() ʱ����AE�ij���
ʱ����AE�ij���
��3����![]() ʱ����AG�ij�.
ʱ����AG�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η��̣�x��3����x��2��=|m|��
��1����֤����������ʵ��m������������������ȵ�ʵ������
��2�������̵�һ������1����m��ֵ�����̵���һ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ1�������������У�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��˳ʱ����ת
��˳ʱ����ת![]() ��
��![]() ����
����![]() ���
���![]() ��Ӧ��.
��Ӧ��.
��1��ֱ��д��![]() ��ֵ��
��ֵ��![]() ��
��
��2�����̶�ֱ��������![]() ��ֱ��д��
��ֱ��д��![]() �����꣨������ͼ�ۼ�����д��������
�����꣨������ͼ�ۼ�����д��������
��3�������![]() ��
��![]() �Ľ�ƽ�����ϣ������ĸ��
�Ľ�ƽ�����ϣ������ĸ��![]() ����������
����������![]() �У� ����ֱ��д���𰸣�
�У� ����ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ��߸��ϵ�C��������CE��CF�̶����߸ˣ�����CE�͵����60���ǣ�������߸�6��B�����ò���ǣ���A����õ��߸���C��������Ϊ30������֪����Ǹ�ABΪ1.5�ף�������CE�ij�������������ţ���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com