
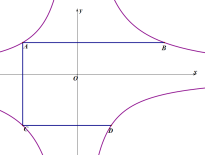
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§y=Љx2+bx+cЕФЭМЯѓгыxжсНЛгкЕуA(Љ1ЃЌ0)ЃЌB(2ЃЌ0)ЃЌгыyжсЯрНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуEЪЧЕквЛЯѓЯоЕФХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЕБЫФБпаЮABECЕФУцЛ§зюДѓЪБЃЌЧѓЕуEЕФзјБъЃЌВЂЧѓГіЫФБпаЮABECЕФзюДѓУцЛ§ЃЛ
ЃЈ3ЃЉШєЕуMдкХзЮяЯпЩЯЃЌЧвдкyжсЕФгвВрЃЎЁбMгыyжсЯрЧаЃЌЧаЕуЮЊDЃЎвдCЃЌDЃЌMЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOCЯрЫЦЃЌЧыжБНгаДГіЕуMЕФзјБъЃЎ
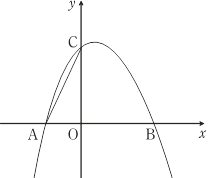
ЁОД№АИЁПЃЈ1ЃЉЖўДЮКЏЪ§ЕФНтЮіЪНЮЊy=Љx2+x+2ЃЛЃЈ2ЃЉЕуEЕФзјБъЮЊ(1ЃЌ2)ЃЌЧвЫФБпаЮABECЕФзюДѓУцЛ§ЮЊ4ЃЛЃЈ3ЃЉЕуMЕФзјБъЮЊ(![]() ЃЌ
ЃЌ ![]() )ЃЌ(
)ЃЌ(![]() ЃЌ
ЃЌ ![]() )ЃЌ(3ЃЌЃ4) .
)ЃЌ(3ЃЌЃ4) .
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉАбAЁЂBЕФзјБъДњШыМДПЩЕУЕНД№АИЃЛ
ЃЈ2ЃЉЩш EЃЈaЃЌbЃЉЃЌЯШБэЪОГіЫФБпаЮABECЕФУцЛ§SЃЌдйХфЗНМДПЩЃЛ
ЃЈ3ЃЉЗжСНжжЧщПіЬжТлЃЌ ![]() ЃЌЛђ
ЃЌЛђ![]() ЃЎ
ЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЁп ЖўДЮКЏЪ§![]() ЕФЭМЯѓгыxжсЯрНЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌ
ЕФЭМЯѓгыxжсЯрНЛгкЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌ
Ёр![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК ![]() ЃЌЁр ЖўДЮКЏЪ§ЕФНтЮіЪНЮЊ
ЃЌЁр ЖўДЮКЏЪ§ЕФНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ1ЃЎ
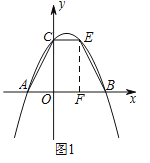
ЁпЖўДЮКЏЪ§ЕФНтЮіЪНЮЊ![]() гыyжсЯрНЛгкЕуCЃЌЁр CЃЈ0ЃЌ2ЃЉЃЌЩш EЃЈaЃЌbЃЉЃЌЧвa >0ЃЌb >0ЃЌЁп AЃЈ-1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌЁр OA=1ЃЌOB=2ЃЌOC=2ЃЌдђSЫФБпаЮABEC=
гыyжсЯрНЛгкЕуCЃЌЁр CЃЈ0ЃЌ2ЃЉЃЌЩш EЃЈaЃЌbЃЉЃЌЧвa >0ЃЌb >0ЃЌЁп AЃЈ-1ЃЌ0ЃЉЃЌBЃЈ2ЃЌ0ЃЉЃЌЁр OA=1ЃЌOB=2ЃЌOC=2ЃЌдђSЫФБпаЮABEC= ![]() =
= ![]() ЃЌЁп Еу EЃЈaЃЌbЃЉЪЧЕквЛЯѓЯоЕФХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЁр
ЃЌЁп Еу EЃЈaЃЌbЃЉЪЧЕквЛЯѓЯоЕФХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЁр![]() ЃЌЁр
ЃЌЁр![]() ЃЌЁр ЕБЫФБпаЮABECЕФУцЛ§зюДѓЪБЃЌЕуEЕФзјБъЮЊЃЈ1ЃЌ4ЃЉЃЌЧвЫФБпаЮABECЕФзюДѓУцЛ§ЮЊ4ЃЛ
ЃЌЁр ЕБЫФБпаЮABECЕФУцЛ§зюДѓЪБЃЌЕуEЕФзјБъЮЊЃЈ1ЃЌ4ЃЉЃЌЧвЫФБпаЮABECЕФзюДѓУцЛ§ЮЊ4ЃЛ
ЃЈ3ЃЉШчЭМ2ЃЎ
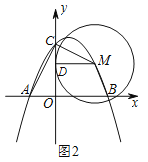
ЩшMЃЈmЃЌnЃЉЃЌЧвm>0ЃЌЁп ЕуMдкЖўДЮКЏЪ§ЕФЭМЯѓЩЯЃЌЁр![]() ЃЌЁп ЁбMгыyжсЯрЧаЃЌЧаЕуЮЊDЃЌЁр ЁЯMDC =90ЁуЃЌЁп вдCЃЌDЃЌMЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOCЯрЫЦЃЌЁр
ЃЌЁп ЁбMгыyжсЯрЧаЃЌЧаЕуЮЊDЃЌЁр ЁЯMDC =90ЁуЃЌЁп вдCЃЌDЃЌMЮЊЖЅЕуЕФШ§НЧаЮгыЁїAOCЯрЫЦЃЌЁр![]() ЃЌЛђ
ЃЌЛђ![]() ЃЌ
ЃЌ
ЂйЕБn >2ЪБЃЌ ![]() ЃЌНтЕУ m1=0ЃЈЩсШЅЃЉЃЌm2=
ЃЌНтЕУ m1=0ЃЈЩсШЅЃЉЃЌm2=![]() ЃЌ Лђm3=0ЃЈЩсШЅЃЉЃЌm4=-1ЃЈЩсШЅЃЉЃЛ
ЃЌ Лђm3=0ЃЈЩсШЅЃЉЃЌm4=-1ЃЈЩсШЅЃЉЃЛ
ЂкЭЌРэПЩЕУЃЌЕБn<2ЪБЃЌm1=0ЃЈЩсШЅЃЉ ЃЌm2=![]() ЃЌЛђm3=0ЃЈЩсШЅЃЉЃЌm4=3ЃЛ
ЃЌЛђm3=0ЃЈЩсШЅЃЉЃЌm4=3ЃЛ
злЩЯЃЌТњзуЬѕМўЕФЕуMЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌЃЈ
ЃЉЃЌЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌЃЈ3ЃЌ-4ЃЉЃЎ
ЃЉЃЌЃЈ3ЃЌ-4ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
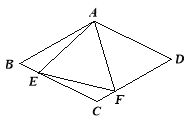
ЁОЬтФПЁПШчЭМЫљЪОЃЌADЪЧЁїABCЕФжаЯпЃЌAEЁЭABЃЌAFЁЭACЃЌЧвAE=ABЃЌAF=ACЃЌAD=3ЃЌAB=4ЃЎ

ЃЈ1ЃЉЧѓACГЄЖШЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЧѓEFЕФГЄЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧыФуЛГівЛИівдBCЮЊЕзБпЕФЕШбќІЄABCЃЌЪЙЕзБпЩЯЕФИпAD=BCЃЎ
ЃЈ1ЃЉЧѓtanBКЭ sinBЕФжЕЃЛ
ЃЈ2ЃЉдкФуЫљЛЕФЕШбќІЄABCжаЩшЕзБпBC=5УзЃЌЧѓбќЩЯЕФИпBEЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУ4ИіГЄ7РхУзЁЂПэ2РхУзЕФГЄЗНаЮЦДГЩвЛИіДѓГЄЗНаЮ(ШчЭМ,зѓЯТНЧКЭгвЩЯНЧжиЕў)ЃЌДѓГЄЗНаЮЕФжмГЄЪЧЖрЩйРхУз?ЭМжавѕгАВПЗжЕФУцЛ§ЪЧЖрЩйЦНЗНРхУз?
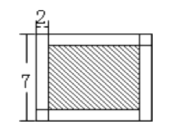
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌAЁЂDдкЗДБШР§КЏЪ§![]()
![]() ЕФЭМЯёЩЯЃЌЕуBЁЂCдкЗДБШР§КЏЪ§
ЕФЭМЯёЩЯЃЌЕуBЁЂCдкЗДБШР§КЏЪ§![]() ЕФЭМЯёЩЯЃЌШєABЁЮCDЁЮ
ЕФЭМЯёЩЯЃЌШєABЁЮCDЁЮ![]() жсЃЌ
жсЃЌ![]() ЁЮ
ЁЮ![]() жсЃЌЧв
жсЃЌЧв![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() =______ЃЎ
=______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїгУ12дЊТђШэУцБЪМЧБОЃЌаЁРігУ21дЊТђгВУцБЪМЧБОЃЎ
ЃЈ1ЃЉвбжЊУПБОгВУцБЪМЧБОБШШэУцБЪМЧБОЙѓ1.2дЊЃЌаЁУїКЭаЁРіФмТђЕНЯрЭЌЪ§СПЕФБЪМЧБОТ№ЃП
ЃЈ2ЃЉвбжЊУПБОгВУцБЪМЧБОБШШэУцБЪМЧБОЙѓaдЊЃЌЪЧЗёДцдке§ећЪ§aЃЌЪЙЕУУПБОгВУцБЪМЧБОЁЂШэУцБЪМЧБОЕФМлИёЖМЪЧе§ећЪ§ЃЌВЂЧваЁУїКЭаЁРіФмТђЕНЯрЭЌЪ§СПЕФБЪМЧБОЃПШєДцдкЃЌЧѓГіaЕФжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЯТСаИїЬтЃК
ЃЈ1ЃЉ![]()
ЃЈ2ЃЉ(![]() Ѓ
Ѓ![]() Ѓ
Ѓ![]() ЃЋ
ЃЋ![]() )ЁС24
)ЁС24
ЃЈ3ЃЉ![]()
ЃЈ4ЃЉ-18ЁТ(-3)+5ЁС(![]() )-(-15)ЁТ5
)-(-15)ЁТ5
ЃЈ5ЃЉ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЬхг§гУЦЗЩЬГЁдЄВтФГЦЗХЦдЫЖЏЗўФмЙЛГЉЯњЃЌОЭгУ32000дЊЙКНјСЫвЛХњетжждЫЖЏЗўЃЌЩЯЪаКѓКмПьЭбЯњЃЌЩЬГЁгжгУ68000дЊЙКНјЕкЖўХњетжждЫЖЏЗўЃЌЫљЙКЪ§СПЪЧЕквЛХњЙКНјЪ§СПЕФ2БЖЃЌЕЋУПЬзНјМлЖрСЫ10дЊЃЎ
ЃЈ1ЃЉИУЩЬГЁСНДЮЙВЙКНјетжждЫЖЏЗўЖрЩйЬзЃП
ЃЈ2ЃЉШчЙћетСНХњдЫЖЏЗўУПЬзЕФЪлМлЯрЭЌЃЌЧвШЋВПЪлЭъКѓзмРћШѓВЛЕЭгк20%ЃЌФЧУДУПЬзЪлМлжСЩйЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкСтаЮABCDжаЃЌAB=4ЃЌЁЯBAD=120ЁуЃЌЁїAEFЮЊе§Ш§НЧаЮЃЌЕуEЁЂFЗжБ№дкСтаЮЕФБпBCЁЂCDЩЯЛЌЖЏЃЌЧвEЁЂFВЛгыBЁЂCЁЂDжиКЯЃЎ
ЃЈ1ЃЉжЄУїВЛТлEЁЂFдкBCЃЎCDЩЯШчКЮЛЌЖЏЃЌзмгаBE=CFЃЛ
ЃЈ2ЃЉЕБЕуEЁЂFдкBCЃЎCDЩЯЛЌЖЏЪБЃЌЗжБ№ЬНЬжЫФБпаЮAECFЕФУцЛ§КЭЁїCEFЕФжмГЄЪЧЗёЗЂЩњБфЛЏЃПШчЙћВЛБфЃЌЧѓГіетИіЖЈжЕЃЛШчЙћБфЛЏЃЌЧѓГізюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com