
����Ŀ��������![]() ��
��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ��
��
��1��ֱ��д��������![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����ͼ1����![]() ��
��![]() ������������
������������![]() �ϣ�����
�ϣ�����![]() ������ƽ��4����λ���ȣ�������ƽ��
������ƽ��4����λ���ȣ�������ƽ��![]() ����λ���ȣ��õ��Ķ�Ӧ��
����λ���ȣ��õ��Ķ�Ӧ��![]() ǡ������������
ǡ������������![]() �ϣ���
�ϣ���![]() �����
�����![]() �����ꣻ
�����ꣻ
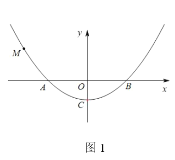
��3����ͼ2����������![]() ����ƽ��2����λ���ȵõ�������
����ƽ��2����λ���ȵõ�������![]() ��һ�κ���
��һ�κ���![]() ��ͼ��
��ͼ��![]() ��������
��������![]() ֻ��һ��������
ֻ��һ��������![]() ����
����![]() �ύ�ڵ�
�ύ�ڵ�![]() ��̽����
��̽����![]() �����Ƿ���ڶ���
�����Ƿ���ڶ���![]() ����
����![]() �������ڣ������
�������ڣ������![]() �����ꣻ����˵�����ɣ�
�����ꣻ����˵�����ɣ�
���𰸡���1��![]() ����2��
����2��![]() ��
��![]() ����3�����ڣ�
����3�����ڣ�![]()
��������
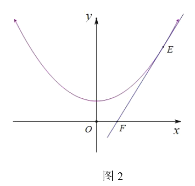
��1���������⣬�����B�����꣬Ȼ��B��C��������������ߵĽ���ʽ�м���������ۣ�
��2����![]() ����
����![]() �����ô���ϵ�������ֱ��MC�Ľ���ʽ������
�����ô���ϵ�������ֱ��MC�Ľ���ʽ������![]() ��
��![]() �ύ
�ύ![]() ��
��![]() �����ݵ�N��y���λ�ù�ϵ�������ۣ����á�Ǧ���ߣ�ˮƽ�����г����̣�����������ۣ�
�����ݵ�N��y���λ�ù�ϵ�������ۣ����á�Ǧ���ߣ�ˮƽ�����г����̣�����������ۣ�
��3����������ɵ�ƽ�ƺ�Ķ��κ�������ʽΪ![]() ����
����![]() �����ֱ��l�Ľ���ʽ��Ȼ���������̣����=0�������
�����ֱ��l�Ľ���ʽ��Ȼ���������̣����=0�������![]() ������
������![]() ��
��![]() ��
��![]() ���Ƕ���
���Ƕ���![]() ������
������![]() ��
��![]() ���������������ε��ж�֤��
���������������ε��ж�֤��![]() ���г�����ʽ����������ۣ�
���г�����ʽ����������ۣ�
�⣺��1����![]()
��OC=1
��AB=4OC
��AB=4
�������ߵĶԳ���Ϊy��
��OB=2
���B��������2,0��
����B��C���������![]() ����
����
![]()
��������![]() �Ľ���ʽΪ
�Ľ���ʽΪ![]() ��
��
��2���⣺����![]() ����
����![]() ��
��
![]() ��
��
![]() ��
��![]() ��
��
����N��������룬��
�ɵã�![]() ��
��
����![]() ��
��![]() �ύ
�ύ![]() ��
��![]() ��
��
![]() ��
��
���һ������![]() ��
��![]() �����ʱ����
�����ʱ����![]()
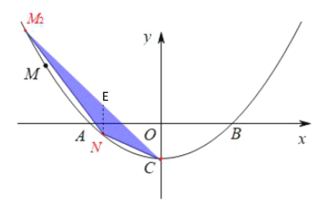
��![]()
![]()
��ã�![]() ��
��![]() ����ȥ����
����ȥ����
���ʱM![]()
�����������![]() ��
��![]() ���Ҳ�ʱ����
���Ҳ�ʱ����![]()
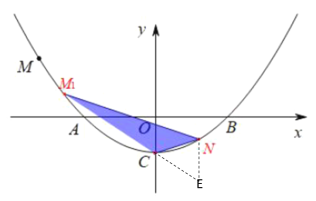
��![]()
![]()
��ã�![]()
���ʱ![]()
���ϣ�![]() ��
��![]() ��
��
��3���⣺���ڣ�
�������֪��ƽ�ƺ�Ķ��κ�������ʽΪ![]()
���������![]() ��
��
��![]() ����l��
����l��
�ɵ�![]() ��
��![]()
����
�����ã�![]()
![]()
![]()
��![]() ��
��![]()
��![]() ʱ����
ʱ����![]()
![]()
����![]() ��
��![]() ��
��![]() ���Ƕ���
���Ƕ���![]() ������
������![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
���HEG����EGH=90�㣬��OGF����EGH=90��
���HEG=��OGF
![]() ��
��
![]()
 ��
��
��ã�![]() ��
��![]() ����GΪ���㣬����ȥ��
����GΪ���㣬����ȥ��
![]() ��
��




| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ��
�����Ķ�����ת���ǽ�ͼ���ϵ�ÿһ����ƽ����������ת������ת�̶��Ƕȵ�λ���ƶ��������������ǹ��̣���ת���ǽ������ת��Ϊͼ�α任��һ�֣��߱�ͼ����תǰ���Ӧ�㵽��ת���ĵľ�����ȣ���Ӧ������ת���������߶εļнǵ�����ת�ǣ���תǰ�����ͼ����ȫ��ͼ�ε����ʣ����Գ��������Щ�������ڽ���й���ת����Ĺؽ���
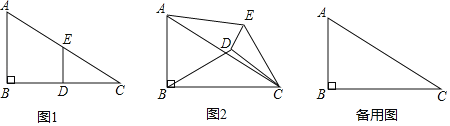
ʵ����������ͼ1����Rt��ABC�У���B��90����BC��2AB��12����D��E�ֱ��DZ�BC��AC���е㣬����DE������EDC�Ƶ�C��˳ʱ�뷽����ת������ת��Ϊ����
����������1���ٵ�����0��ʱ��![]() ���� �����ڵ�����180��ʱ��
���� �����ڵ�����180��ʱ��![]() ���� ����
���� ����
��2�����жϣ���0���a��360��ʱ��![]() �Ĵ�С���ޱ仯�������ͼ2�����θ���֤����
�Ĵ�С���ޱ仯�������ͼ2�����θ���֤����
������̽����3������EDC��ת��A��D��E���㹲��ʱ������߶�BD�ij�Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ABC��90�㣬C��0����4����AC��3AD����A�ڷ���������y��![]() ͼ���ϣ���y��ƽ�֡�ACB����k��_��
ͼ���ϣ���y��ƽ�֡�ACB����k��_��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
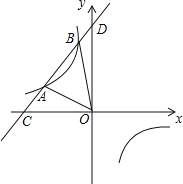
����Ŀ����ͼ��ʾ��ֱ��AB��˫����y��![]() ����A��B���㣬ֱ��AB��x��y������ֱ���C��D���㣬����OA����OA��2
����A��B���㣬ֱ��AB��x��y������ֱ���C��D���㣬����OA����OA��2![]() ��tan��AOC��
��tan��AOC��![]() ��B(��3��m)
��B(��3��m)
��1���ֱ���һ�κ����뷴��������ʽ��
��2������OB����x�������P�����꣬ʹ��AOP�����������AOB�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
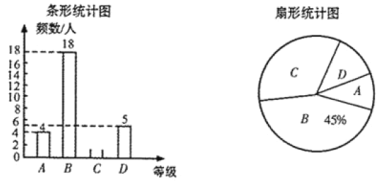
����Ŀ��2020��2��10�գ�������ѧ��ί��������ƽ̨��֯���꼶600��ѧ���μ���ȫ������֪ʶ������Ϊ���˽Ȿ�δ����ijɼ��������ȡ�˲���ѧ���ijɼ���Ϊ��������![]() ��
��![]() ��
��![]() ��
��![]() �ĸ��ȼ�����ͳ�ƣ��Ƴ����²�������ͳ��ͼ��
�ĸ��ȼ�����ͳ�ƣ��Ƴ����²�������ͳ��ͼ��
��˵����![]() ��80��-100�֣�
��80��-100�֣�![]() ��70��-79�֣�
��70��-79�֣�![]() ��60-69�֣�
��60-69�֣�![]() ��0��-59�֣�
��0��-59�֣�
����������Ϣ������������⣺
��1��������ͳ��ͼ�У�![]() ����Ӧ�����ε�Բ�Ľ���______�ȣ�
����Ӧ�����ε�Բ�Ľ���______�ȣ�
��2����ȫ����ͳ��ͼ��
��3������ȡѧ��������������Գɼ�����λ��������______�ȼ���
��4�����ɼ��ﵽ![]() �ȼ���ѧ������ѡΪ־Ը�ߣ�����Ƹ�У���꼶600��ѧ���п���ѡΪ־Ը��ѧ���ж����ˣ�
�ȼ���ѧ������ѡΪ־Ը�ߣ�����Ƹ�У���꼶600��ѧ���п���ѡΪ־Ը��ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() �У�
��![]() ��
��![]() ���е㣬��
���е㣬��![]() ��
��![]() �ϣ���
�ϣ���![]() ����
����![]() �غϣ�������
�غϣ�������![]() ��ֱ�߽�
��ֱ�߽�![]() ��
��![]() ��������
��������![]() �ڵ�
�ڵ�![]() ����
����![]() ��
��![]() ��
��
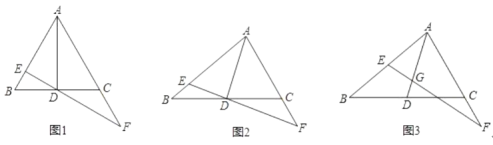
��1����ͼ1����![]() Ϊ�ȱ������Σ���
Ϊ�ȱ������Σ���![]() ��
��![]() �غϣ�
�غϣ�![]() ����֤��
����֤��![]() ��
��
��2����ͼ2������![]() ��
��![]() �غϣ���֤��
�غϣ���֤��![]() ��
��
��3����ͼ3����![]() ��
��![]() ��
��![]() ��ֱ��д��
��ֱ��д��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���E�DZ�BC���е㣬����AE���ӳ�����DC���ӳ����ڵ�F������AC��BF.
��1����֤����ABE�ա�FCE��
��2�����ı���ABFC�Ǿ���ʱ������AEC=80�㣬���D�Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y����![]() x+2��ͼ����x�ᡢy��ֱ��ڵ�A��B�����߶�ABΪ���ڵ�һ�������ȱ���ABC��
x+2��ͼ����x�ᡢy��ֱ��ڵ�A��B�����߶�ABΪ���ڵ�һ�������ȱ���ABC��
��1������C�ڷ���������y��![]() ��ͼ���ϣ���÷����������Ľ���ʽ��
��ͼ���ϣ���÷����������Ľ���ʽ��
��2����P��4![]() ��m���ڵ�һ���ޣ�����P��x��Ĵ��ߣ�����ΪD������PAD����OAB������P���ڣ�1���з���������ͼ����ʱ�����P�����꣮
��m���ڵ�һ���ޣ�����P��x��Ĵ��ߣ�����ΪD������PAD����OAB������P���ڣ�1���з���������ͼ����ʱ�����P�����꣮
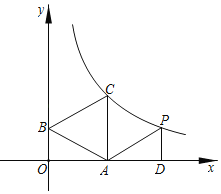
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD������E��AC�ϣ�AF��AC������ΪA��AF��AE��
��1��BF��DE��������������ϵ����֤����Ľ��ۣ�
��2�����������������ֲ����������£�����E�˶���AC�е�ʱ���ı���AFBE��ʲô�����ı��Σ���֤����Ľ��ۣ�
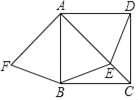
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com