【题目】附加题：如图，已知∠1=∠2，∠3=∠4，∠A=100°，求x的值．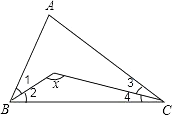 
【答案】解：∵在△ABC中，∠A+∠ABC+∠ACB=180°，∠A=100°， ∴∠ABC+∠ACB=180°﹣100°=80°，
∵∠1=∠2，∠3=∠4，
∴∠2+∠4= 
（∠ABC+∠ACB）=40°，
∴x=180°﹣（∠2+∠4）=140°．
【解析】根据的是三角形内角和定理以及角平分线性质解答即可．
【考点精析】认真审题，首先需要了解角的平分线(从一个角的顶点引出的一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线)，还要掌握三角形的内角和外角(三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角)的相关知识才是答题的关键．
科目：初中数学 来源： 题型：
【题目】一个数能否被99整除是从这个数的末位开始，两位一段，看看这些数段的和能否被99整除。像这样能够被99整除的数，我们称之为“长久数”。例如542718,因为18+27+54=99，所以542718能够被99整除；又例如25146,因为46+51+2=99，所以25146能够被99整除。
（1）若
这个三位数是“长久数”，求a的值；
（2）在（1）中的三位数的首位和个位与十位之间加上和为9的两个数字，让其成为一个五位数，该五位数仍是“长久数”，求这个五位数；
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在□ABCD中，点E、F分别是AD、BC的中点，分别连接BE、DF、BD．
（1）求证：△AEB≌△CFD；
（2）若四边形EBFD是菱形，求∠ABD的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】（本题满分12分）已知：点E为AB边上的一个动点.
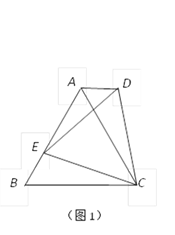
（1）如图1，若△ABC是等边三角形，以CE为边在BC的同侧作等边△DEC ，连结AD.试比较∠DAC与∠B的大小，并说明理由；
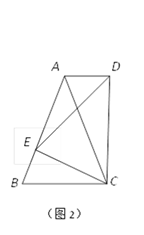
（2）如图2，若△ABC中，AB=AC，以CE为底边在BC的同侧作等腰△DEC ，且
△DEC∽△ABC，连结AD.试判断AD与BC的位置关系，并说明理由；
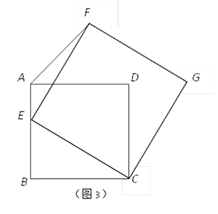
（3）如图3，若四边形ABCD是边长为2的正方形，以CE为边在BC的同侧作正方形ECGF.
①试说明点G一定在AD的延长线上；
②当点E在AB边上由点B运动至点A时，点F随之运动，求点F的运动路径长.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在数学表达式：①-2＜0； ②3x-5＞0； ③ x=1； ④x2-x ；⑤x≠-2 ；⑥x+2＞x-1中，不等式有（ ）.
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如果两个三角形的两边及其中一边的对角对应相等，那么这两个三角形全等，其逆命题是_______________________，这个逆命题是________命题．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com