
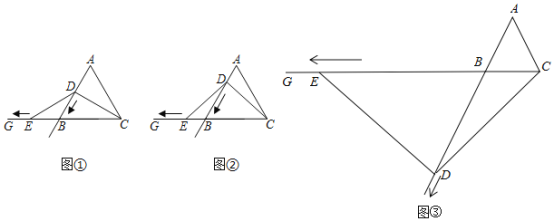
ЁОЬтФПЁПШчЭМЃЌЁїABCЪЧЕШБпШ§НЧаЮЃЌЕуDЁЂEЗжБ№ЪЧЩфЯпABЁЂЩфЯпCBЩЯЕФЖЏЕуЃЌЕуDДгЕуAГіЗЂбиЩфЯпABвЦЖЏЃЌЕуEДгЕуBГіЗЂбиBGвЦЖЏЃЌЕуDЁЂЕуEЭЌЪБГіЗЂВЂЧвдЫЖЏЫйЖШЯрЭЌЃЎСЌНгCDЁЂDEЃЎ
ЃЈ1ЃЉШчЭМЂйЃЌЕБЕуDвЦЖЏЕНЯпЖЮABЕФжаЕуЪБЃЌЧѓжЄЃКDE=DCЃЎ
ЃЈ2ЃЉШчЭМЂкЃЌЕБЕуDдкЯпЖЮABЩЯвЦЖЏЕЋВЛЪЧжаЕуЪБЃЌЪдЬНЫїDEгыDCжЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШчЭМЂлЃЌЕБЕуDвЦЖЏЕНЯпЖЮABЕФбгГЄЯпЩЯЃЌВЂЧвEDЁЭDCЪБЃЌЧѓЁЯDECЖШЪ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉМћЯъНтЃЛ
ЃЈ2ЃЉDE=DCЃЌРэгЩМћЯъНтЃЛ
ЃЈ3ЃЉЁЯDEC=45Ёу
ЁОНтЮіЁП
ЃЈ1ЃЉгЩЬтвтПЩжЊ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌгЩЕШБпШ§НЧаЮМАжаЕуПЩжЊ
ЃЌгЩЕШБпШ§НЧаЮМАжаЕуПЩжЊ![]() ЃЌЖј
ЃЌЖј![]() ЃЌЫљвдПЩжЄ
ЃЌЫљвдПЩжЄ![]() ЃЌНјвЛВНПЩжЄ
ЃЌНјвЛВНПЩжЄ![]()
ЃЈ2ЃЉВТВт![]() ЃЌбАевЬѕМўжЄУїМДПЩ.зюГЃгУЕФЪЧжЄУїСНИіШ§НЧаЮШЋЕШЃЌЕЋЭМжаИјГіЕФШ§НЧаЮжаВЂЮДГіЯжШЋЕШШ§НЧаЮЃЌЫљвдЬэМгИЈжњЯпЃКдкЩфЯпABЩЯНиШЁ
ЃЌбАевЬѕМўжЄУїМДПЩ.зюГЃгУЕФЪЧжЄУїСНИіШ§НЧаЮШЋЕШЃЌЕЋЭМжаИјГіЕФШ§НЧаЮжаВЂЮДГіЯжШЋЕШШ§НЧаЮЃЌЫљвдЬэМгИЈжњЯпЃКдкЩфЯпABЩЯНиШЁ![]() ЃЌетбљжЛвЊжЄУї
ЃЌетбљжЛвЊжЄУї![]() МДПЩ.РћгУЕШБпШ§НЧаЮЕФаджЪМА
МДПЩ.РћгУЕШБпШ§НЧаЮЕФаджЪМА![]() ПЩжЊ
ПЩжЊ![]() ЮЊЕШБпШ§НЧаЮЃЌетбљЭЈЙ§СНИіЕШБпШ§НЧаЮМДПЩжЄУї
ЮЊЕШБпШ§НЧаЮЃЌетбљЭЈЙ§СНИіЕШБпШ§НЧаЮМДПЩжЄУї![]() .
.
ЃЈ3ЃЉАДееЕкЃЈ2ЃЉЮЪЕФЫМТЗЃЌзїГіРрЫЦЕФИЈжњЯпЃКдкЩфЯпCBЩЯНиШЁ![]() ЃЌгУЭЌбљЕФЗНЗЈжЄУї
ЃЌгУЭЌбљЕФЗНЗЈжЄУї![]() ЃЌгжвђЮЊEDЁЭDCЃЌЫљвд
ЃЌгжвђЮЊEDЁЭDCЃЌЫљвд![]() ЮЊЕШбќжЎМфШ§НЧаЮЃЌдђЁЯDECЖШЪ§ПЩЧѓ.
ЮЊЕШбќжЎМфШ§НЧаЮЃЌдђЁЯDECЖШЪ§ПЩЧѓ.
гЩЬтвтПЩжЊ![]()
ЁпDЮЊABЕФжаЕу
![]()
![]()
![]()
Ёп![]() ЮЊЕШБпШ§НЧаЮЃЌ
ЮЊЕШБпШ§НЧаЮЃЌ![]()
![]()
![]()
![]()
![]()
![]()
ЃЈ2ЃЉ![]()
РэгЩШчЯТЃК
дкЩфЯпABЩЯНиШЁ![]() ЃЌСЌНгEF
ЃЌСЌНгEF

Ёп![]() ЮЊЕШБпШ§НЧаЮ
ЮЊЕШБпШ§НЧаЮ
![]()
![]()
Ёр![]() ЮЊЕШБпШ§НЧаЮ
ЮЊЕШБпШ§НЧаЮ
![]()
гЩЬтвтжЊ![]()
![]()
![]()
МД![]()
![]()
![]()
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ
![]()
![]()
ЃЈ3ЃЉШчЭМЃЌдкЩфЯпCBЩЯНиШЁ![]() ЃЌСЌНгDF
ЃЌСЌНгDF

Ёп![]() ЮЊЕШБпШ§НЧаЮ
ЮЊЕШБпШ§НЧаЮ
![]()
![]()
Ёр![]() ЮЊЕШБпШ§НЧаЮ
ЮЊЕШБпШ§НЧаЮ
![]()
![]()
гЩЬтвтжЊ![]()
![]()
![]()
МД![]()
![]()
![]()
дк![]() КЭ
КЭ![]() жаЃЌ
жаЃЌ
![]()
![]()
ЁпEDЁЭDC
Ёр![]() ЮЊЕШбќжБНЧШ§НЧаЮ
ЮЊЕШбќжБНЧШ§НЧаЮ
![]()


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖўДЮКЏЪ§![]() ЕФВПЗжЭМЯѓШчЭМЫљЪОЃЌЦфжаЭМЯѓгы
ЕФВПЗжЭМЯѓШчЭМЫљЪОЃЌЦфжаЭМЯѓгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌгы
ЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЧвОЙ§Еу
ЃЌЧвОЙ§Еу![]() ЃЎ
ЃЎ

![]() ЧѓДЫЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЧѓДЫЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
![]() НЋДЫЖўДЮКЏЪ§ЕФНтЮіЪНаДГЩ
НЋДЫЖўДЮКЏЪ§ЕФНтЮіЪНаДГЩ![]() ЕФаЮЪНЃЌВЂжБНгаДГіЖЅЕузјБъвдМАЫќгы
ЕФаЮЪНЃЌВЂжБНгаДГіЖЅЕузјБъвдМАЫќгы![]() жсЕФСэвЛИіНЛЕу
жсЕФСэвЛИіНЛЕу![]() ЕФзјБъЃЎ
ЕФзјБъЃЎ
![]() РћгУвдЩЯаХЯЂНтД№ЯТСаЮЪЬтЃКШєЙигк
РћгУвдЩЯаХЯЂНтД№ЯТСаЮЪЬтЃКШєЙигк![]() ЕФвЛдЊЖўДЮЗНГЬ
ЕФвЛдЊЖўДЮЗНГЬ![]() ЃЈ
ЃЈ![]() ЮЊЪЕЪ§ЃЉдк
ЮЊЪЕЪ§ЃЉдк![]() ЕФЗЖЮЇФкгаНтЃЌдђ
ЕФЗЖЮЇФкгаНтЃЌдђ![]() ЕФШЁжЕЗЖЮЇЪЧ________ЃЎ
ЕФШЁжЕЗЖЮЇЪЧ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћШЮвтбЁдёвЛЖдгаађећЪ§(mЃЌn)ЃЌЦфжа|m|Ём1ЃЌ|n|Ём3ЃЌУПвЛЖдетбљЕФгаађећЪ§БЛбЁдёЕФПЩФмадЪЧЯрЕШЕФЃЌФЧУДЙигкxЕФЗНГЬx2ЃЋnxЃЋmЃН0гаСНИіЯрЕШЪЕЪ§ИљЕФИХТЪЪЧ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌЁїABCжаЃЌADЪЧЁЯBACЕФНЧЦНЗжЯпЃЌШєAB=AC+CD.ФЧУДЁЯACB гыЁЯABCгадѕбљЕФЪ§СПЙиЯЕ? аЁУїЭЈЙ§ЙлВьЗжЮіЃЌаЮГЩСЫШчЯТНтЬтЫМТЗ:
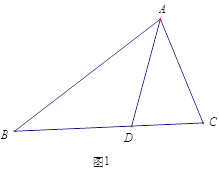
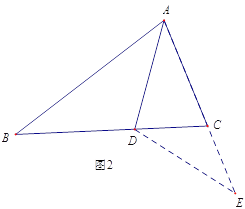
ШчЭМ2,бгГЄACЕНE,ЪЙCE=CD,СЌНгDE,гЩAB=AC+CD,ПЩЕУAE=AB,гжвђЮЊADЪЧЁЯBACЕФЦНЗжЯпЃЌПЩЕУЁїABDЁеЁїAED,НјвЛВНЗжЮіОЭПЩвдЕУЕНЁЯACB гыЁЯABCЕФЪ§СПЙиЯЕ.
(1) ХаЖЈЁїABD гыЁїAED ШЋЕШЕФвРОнЪЧ______________(SSS,SAS,ASA,AAS ДгЦфжабЁдёвЛИі);
(2)ЁЯACB гыЁЯABCЕФЪ§СПЙиЯЕЮЊ:___________________
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊМгЧПаЃдАбєЙтЬхг§ЛюЖЏЃЌФГжабЇМЦЛЎЙКНјвЛХњРКЧђКЭХХЧђЃЌОЙ§ЕїВщЕУжЊУПИіРКЧђЕФМлИёБШУПИіХХЧђЕФМлИёЙѓ40дЊЃЌТђ5ИіРКЧђКЭ10ИіХХЧђЙВгУ1100дЊЃЎ
ЃЈ1ЃЉЧѓУПИіРКЧђКЭХХЧђЕФМлИёЗжБ№ЪЧЖрЩйЃП
ЃЈ2ЃЉФГбЇаЃашЙКНјРКЧђКЭХХЧђЙВ120ИіЃЌзмЗбгУВЛГЌЙ§9000дЊЃЌЕЋВЛЕЭгк8900дЊЃЌЮЪгаМИжжЙКТђЗНАИЃПзюЕЭЗбгУЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁїABCЕФШ§БпaЃЌbЃЌcЃЌТњзуa+b2+|cЉ6|+28=4![]() +10bЃЌдђЁїABCЕФЭтНгдВАыОЖ=__________ЃЎ
+10bЃЌдђЁїABCЕФЭтНгдВАыОЖ=__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫЗсИЛбЇЩњЕФаЃдАЩњЛюЃЌзМБИЙКНјвЛХњРКЧђКЭзуЧђЃЎЦфжаРКЧђЕФЕЅМлБШзуЧђЕФЕЅМлЖр40дЊЃЌгУ1500дЊЙКНјЕФРКЧђИіЪ§гы900дЊЙКНјЕФзуЧђИіЪ§ЯрЕШЃЎ
ЃЈ1ЃЉРКЧђКЭзуЧђЕФЕЅМлИїЪЧЖрЩйдЊЃП
ЃЈ2ЃЉИУаЃДђЫугУ1000дЊЙКТђРКЧђКЭзуЧђЃЌЮЪЧЁКУгУЭъ1000дЊЃЌВЂЧвРКЧђЁЂзуЧђЖМТђгаЕФЙКТђЗНАИгаФФМИжжЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃКЖдГЦжс![]() ЕФХзЮяЯп
ЕФХзЮяЯп![]() гы
гы![]() жсЯрНЛгк
жсЯрНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌЦфжаЕу
СНЕуЃЌЦфжаЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЧвЕу
ЃЌЧвЕу![]() дкХзЮяЯп
дкХзЮяЯп![]() ЩЯЃЎ
ЩЯЃЎ

![]() ЧѓХзЮяЯпЕФНтЮіЪНЃЎ
ЧѓХзЮяЯпЕФНтЮіЪНЃЎ
![]() Еу
Еу![]() ЮЊХзЮяЯпгы
ЮЊХзЮяЯпгы![]() жсЕФНЛЕуЃЎ
жсЕФНЛЕуЃЎ
ЂйЕу![]() дкХзЮяЯпЩЯЃЌЧв
дкХзЮяЯпЩЯЃЌЧв![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕузјБъЃЎ
ЕузјБъЃЎ
ЂкЩшЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯЕФЖЏЕуЃЌзї
ЩЯЕФЖЏЕуЃЌзї![]() жсНЛХзЮяЯпгкЕу
жсНЛХзЮяЯпгкЕу![]() ЃЌЧѓЯпЖЮ
ЃЌЧѓЯпЖЮ![]() ГЄЖШЕФзюДѓжЕЃЎ
ГЄЖШЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈЮЪЬтБГОАЃЉ
ШчЭМ1ЃЌдкЫФБпаЮADBCжаЃЌЁЯACB=ЁЯADB=90ЁуЃЌAD=BDЃЌЬНОПЯпЖЮACЃЌBCЃЌCDжЎМфЕФЪ§СПЙиЯЕЃЎ
аЁЮтЭЌбЇЬНОПДЫЮЪЬтЕФЫМТЗЪЧЃКНЋЁїBCDШЦЕуDЃЌФцЪБеыа§зЊ90ЁуЕНЁїAEDДІЃЌЕуBЃЌCЗжБ№ТфдкЕуAЃЌEДІЃЈШчЭМ2ЃЉЃЌвзжЄЕуCЃЌAЃЌEдкЭЌвЛЬѕжБЯпЩЯЃЌВЂЧвЁїCDEЪЧЕШбќжБНЧШ§НЧаЮЃЌЫљвдCE=![]() CDЃЌДгЖјЕУГіНсТлЃКAC+BC=
CDЃЌДгЖјЕУГіНсТлЃКAC+BC=![]() CD
CD
ЃЈМђЕЅгІгУЃЉ
ЃЈ1ЃЉдкЭМ1жаЃЌШєAC=3ЃЌ CD=![]() ЃЌдђAB= ЃЎ
ЃЌдђAB= ЃЎ
ЃЈ2ЃЉШчЭМ3ЃЌABЪЧЁбOЕФжБОЖЃЌЕуCЁЂDдкЁбOЩЯЃЌЁЯC=45ЁуЃЌШєAB=13ЃЌBC=12ЃЌЧѓCDЕФГЄЃЎ
ЃЈЭиеЙЙцТЩЃЉ
ЃЈ3ЃЉШчЭМ4ЃЌЁЯACB=ЁЯADB=90ЁуЃЌAD=BDЃЌШєAC=mЃЌCD=nЃЌдђBCЕФГЄЮЊ ЃЎЃЈгУКЌmЃЌnЕФДњЪ§ЪНБэЪОЃЉ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com