




| 5 |
| 2 |
| 15 |
| 2 |
| 5 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| 52-42 |
| 3 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 52-42 |
| 1 |
| 2 |
| 5 |
| 8 |
| 3 |
| 4 |
| 1 |
| 2 |
| 5 |
| 8 |
| 3 |
| 4 |
| 1 |
| 2 |


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
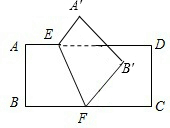 如图,将矩形纸片ABCD沿EF折叠(E、F分别是AD、BC上的点),使点B与四边形CDEF内一点B′重合,若∠B′FC=50°,则∠AEF等于( )
如图,将矩形纸片ABCD沿EF折叠(E、F分别是AD、BC上的点),使点B与四边形CDEF内一点B′重合,若∠B′FC=50°,则∠AEF等于( )| A、110° | B、115° | C、120° | D、130° |
查看答案和解析>>
科目:初中数学 来源: 题型:
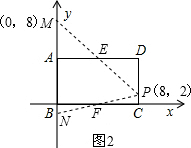
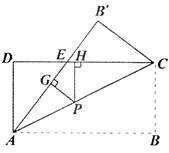
(本题10分)如图,将矩形纸片ABCD沿对角线AC折叠,使点B落到到B′的位置,AB′与CD交于点E.
(1)求证:△AED≌△CEB′
(2)若AB = 8,DE = 3,点P为线段AC上任意一点,PG⊥AE于G,PH⊥BC于H.求PG + PH的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011年江苏省洋思中学九年级月考数学卷 题型:解答题
( 本题满分12分)
【小题1】(1)动手操作:
如图①,将矩形纸片ABCD折叠,使点D与点B重合,点C落在点 处,折痕为EF,若∠ABE=20°,那么
处,折痕为EF,若∠ABE=20°,那么 的度数为 。
的度数为 。
【小题2】(2)观察发现小明将三角形纸片ABC(AB>AC)沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图②);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到△AEF(如图③).小明认为△AEF是等腰三角形,你同意吗?请说明理由
(3)实践与运用:
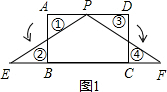
将矩形纸片ABCD 按如下步骤操作:将纸片对折得折痕EF,折痕与AD边交于点E,与BC边交于点F;将矩形ABFE与矩形EFCD分别沿折痕MN和PQ折叠,使点A、点D都与点F重合,展开纸片,此时恰好有MP=MN=PQ(如图④),求∠MNF的大小。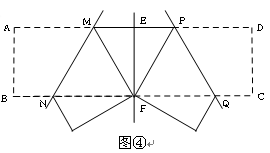
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com