
、请用字母写出等腰梯形ABCD(AD∥BC)特有而一般梯形不具有的两个特征:
① ; ② .
AC=BD;∠B=∠C
解析试题分析:①过D作DM∥AC得到平行四边形ACMD和△DMB,证△ABC≌△DCB得到∠DBC=∠ACB=∠M,根据等角对等边即可得出AC=BD.②首先过D作DE∥AB,把梯形转化成平行四边形和等腰三角形,根据性质即可得出答案.
①证明:过D作DM∥AC交BC的延长线于M,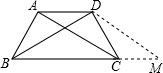
∵AD∥CB,DM∥AC,
∴四边形ACMD是平行四边形,
∴AC=DM,∠ACB=∠M,
∵AD∥BC,AB=DC,
∴∠ABC=∠DCB,
∵BC=BC,AB=DC,
∴△ABC≌△DCB,
∴∠DBC=∠ACB,
∴∠DBC=∠M,
∴DB=DM,
即:AC=BD;
②证明:过D作DE∥AB交BC于E,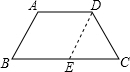
∵AD∥BC,DE∥AB,
∴四边形ABED是平行四边形,
AB=DE,∠B=∠DEC,
∵AB=CD,
∴∠DEC=∠C,
∴∠B=∠C.
考点:本题主要考查了平行四边形的性质和判定,全等三角形的性质和判定,等腰三角形的性质和判定
点评:解此题的关键是作辅助线把梯形转化成平行四边形和等腰三角形.


科目:初中数学 来源: 题型:
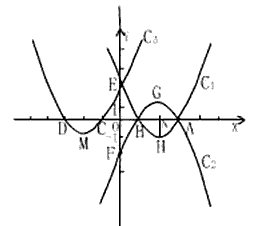
 26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG|
26、已知:如图,抛物线C1,C2关于x轴对称;抛物线C1,C3关于y轴对称.抛物线C1,C2,C3与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线C1,C2,C3的顶点.HN垂直于x轴,垂足为N,且|OE|>|HN|,|AB|≠|HG|查看答案和解析>>
科目:初中数学 来源:期末题 题型:解答题
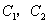 关于
关于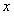 轴对称;抛物线
轴对称;抛物线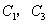 关于y轴对称。抛物线
关于y轴对称。抛物线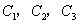 与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线
与x轴相交于A、B、C、D四点;与y相交于E、F两点;H、G、M分别为抛物线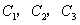 的顶点。HN垂直于x轴,垂足为N,且
的顶点。HN垂直于x轴,垂足为N,且 
查看答案和解析>>
科目:初中数学 来源:第34章《二次函数》中考题集(50):34.4 二次函数的应用(解析版) 题型:解答题
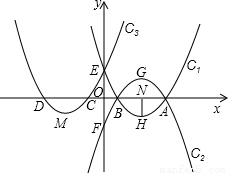 (1)A、B、C、D、E、F、G、H、M9个点中,四个点可以连接成一个四边形,请你用字母写出下列特殊四边形:菱形______;等腰梯形______;平行四边形______;梯形______;(每种特殊四边形只能写一个,写错、多写记0分)
(1)A、B、C、D、E、F、G、H、M9个点中,四个点可以连接成一个四边形,请你用字母写出下列特殊四边形:菱形______;等腰梯形______;平行四边形______;梯形______;(每种特殊四边形只能写一个,写错、多写记0分)查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(48):2.3 二次函数的应用(解析版) 题型:解答题
 (1)A、B、C、D、E、F、G、H、M9个点中,四个点可以连接成一个四边形,请你用字母写出下列特殊四边形:菱形______;等腰梯形______;平行四边形______;梯形______;(每种特殊四边形只能写一个,写错、多写记0分)
(1)A、B、C、D、E、F、G、H、M9个点中,四个点可以连接成一个四边形,请你用字母写出下列特殊四边形:菱形______;等腰梯形______;平行四边形______;梯形______;(每种特殊四边形只能写一个,写错、多写记0分)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com