【答案】
分析:(1)分①当2≤x≤8时,用第八层售价减去楼层差价,②当9≤x≤23时,用第八层售价加上楼层差价,整理即可得解;
(2)求出购买第八层楼的首付款为48000元可知2~8层可任选;第9层以上,根据首付款不大于60000元列出不等式其解即可,然后综合两种情况即可确定出王老师可购买楼层的方案;
(3)根据购买方案二求出实交房款的关系式和按王老师的想法则要交房款的关系式,然后分情况讨论即可确定出a的取值范围.
解答:解:(1)①当2≤x≤8时,每平方米的售价应为:2000-(8-x)×20=20x+1840(元/平方米).
②当9≤x≤23时,每平方米的售价应为:2000+(x-8)•40=40x+1680(元/平方米).
∴y=
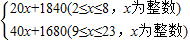
;
(2)由(1)知:
①当2≤x≤8时,王老师首付款为(20x+1840)•80•30%=24(20x+1840),
∵24(20•8+1840)=48000元<60000元,
∴2~8层可任选;
②当9≤x≤23时,王老师首付款为(40x+1680)•80•30%=24(40x+1680)元.
24(40x+1680)≤60000,
解得:x≤20.5.
∵x为正整数,
∴9≤x≤20,
综上得:王老师用方案一可以购买二至二十层的任何一层;
(3)若按方案二购买第十六层,则王老师要实交房款为:
y
1=(40•16+1680)•80•92%-60a(元)
若按王老师的想法则要交房款为:y
2=(40•16+1680)•80•91%(元).
∵y
1-y
2=1856-60a,
∴当y
1>y
2,即y
1-y
2>0时,
解得0<a<
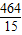
,
此时王老师想法正确;
当y
1≤y
2,即y
1-y
2≤0时,
解得a≥
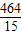
,此时王老师想法不正确.
点评:本题考查的是用一次函数解决实际问题,读懂题目信息,找出数量关系表示出各楼层的单价以及是交房款的关系式是解题的关键.

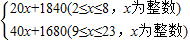 ;
;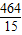 ,
,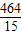 ,此时王老师想法不正确.
,此时王老师想法不正确.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案