
【题目】在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过
经过![]() ,
,![]() 两点.
两点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 在
在![]() 上方的抛物线上有一动点
上方的抛物线上有一动点![]() .
.
①如图![]() ,当点
,当点![]() 运动到某位置时,以
运动到某位置时,以![]() ,
,![]() 为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点
为邻边的平行四边形第四个顶点恰好也在抛物线上,求出此时点![]() 的坐标;
的坐标;
②如图![]() ,过点
,过点![]() ,
,![]() 的直线
的直线![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.

【答案】(1)![]() ;(2)①
;(2)①![]() 点的坐标是
点的坐标是![]() ;②
;②![]() .
.
【解析】
(1)由直线的解析式y=x+4易求点A和点C的坐标,把A和C的坐标分别代入y=-![]() x2+bx+c求出b和c的值即可得到抛物线的解析式;
x2+bx+c求出b和c的值即可得到抛物线的解析式;
(2)①若以AP,AO为邻边的平行四边形的第四个顶点Q恰好也在抛物线上,则PQ∥AO,再根据抛物线的对称轴可求出点P的横坐标,由(1)中的抛物线解析式,进而可求出其纵坐标,问题得解;
②过P点作PF∥OC交AC于点F,因为PF∥OC,所以△PEF∽△OEC,由相似三角形的性质:对应边的比值相等可求出PF的长,进而可设点点F(x,x+4),利用(![]() x2x+4)(x+4)=
x2x+4)(x+4)=![]() ,可求出x的值,解方程求出x的值可得点P的坐标,代入直线y=kx即可求出k的值.
,可求出x的值,解方程求出x的值可得点P的坐标,代入直线y=kx即可求出k的值.
解:![]() ∵直线
∵直线![]() 经过
经过![]() ,
,![]() 两点,
两点,
∴![]() 点坐标是
点坐标是![]() ,点
,点![]() 坐标是
坐标是![]() ,
,
又∵抛物线过![]() ,
,![]() 两点,
两点,
∴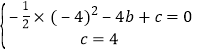 ,解得:
,解得:![]() ,
,
∴抛物线的解析式为![]() .
.
![]() ①如图
①如图![]()
∵![]() ,
,
∴抛物线的对称轴是直线![]() .
.
∵以![]() ,
,![]() 为邻边的平行四边形的第四个顶点
为邻边的平行四边形的第四个顶点![]() 恰好也在抛物线上,
恰好也在抛物线上,
∴![]() ,
,![]() .
.
∵![]() ,
,![]() 都在抛物线上,
都在抛物线上,
∴![]() ,
,![]() 关于直线
关于直线![]() 对称,
对称,
∴![]() 点的横坐标是
点的横坐标是![]() ,
,
∴当![]() 时,
时,![]() ,
,
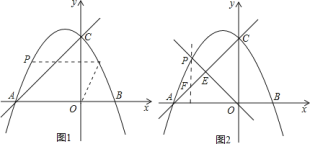
∴![]() 点的坐标是
点的坐标是![]() ;
;
②过![]() 点作
点作![]() 交
交![]() 于点
于点![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
设点![]() ,
,
∴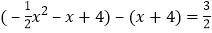 ,
,
化简得:![]() ,解得:
,解得:![]() ,
,![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
即![]() 点坐标是
点坐标是![]() 或
或![]() .
.
又∵点![]() 在直线
在直线![]() 上,
上,
∴![]() .
.


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒
点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒![]() 过点D作
过点D作![]() 于点F,连接DE、EF.
于点F,连接DE、EF.
![]() 求证:
求证:![]() ;
;
![]() 四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
![]() 当t为何值时,
当t为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先列出下列问题中的函数表达式,再指出它们各属于什么函数.
![]() 电压为
电压为![]() 时,电阻
时,电阻![]() 与电流
与电流![]() 的函数关系;
的函数关系;
![]() 食堂每天用煤
食堂每天用煤![]() ,用煤总量
,用煤总量![]() 与用煤天数
与用煤天数![]() (天)的函数关系;
(天)的函数关系;
![]() 积为常数
积为常数![]() 的两个因数
的两个因数![]() 与
与![]() 的函数关系;
的函数关系;
![]() 杠杆平衡时,阻力为
杠杆平衡时,阻力为![]() ,阻力臂长为
,阻力臂长为![]() ,动力
,动力![]() 与动力臂
与动力臂![]() 的函数关系(杠杆本
的函数关系(杠杆本
身所受重力不计).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .较简便的解法是( )
.较简便的解法是( )
A. 依次用直接开平方法、配方法、公式法和因式分解法
B. ①用直接开平方法,②用公式法,③④用因式分解法
C. 依次用因式分解法、公式法、配方法和因式分解法
D. ①用直接开平方法,②③用公式法,④用因式分解法
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
(1)在图中作出![]() 关于
关于![]() 轴对称的
轴对称的![]() .
.
(2)写出点![]() 的坐标(直接写答案).
的坐标(直接写答案).
A1_____________,B1______________,C1______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某幼儿园有一道长为![]() 米的墙,计划用
米的墙,计划用![]() 米长的围栏利用一面墙如图围成一个矩形草坪
米长的围栏利用一面墙如图围成一个矩形草坪![]() .设该矩形草坪
.设该矩形草坪![]() 边的长为
边的长为![]() 米,面积为
米,面积为![]() 平方米.
平方米.
![]() 求出
求出![]() 与
与![]() 的函数关系式并写出
的函数关系式并写出![]() 的取值范围;
的取值范围;
![]()
![]() 如果所围成的矩形草坪面积为
如果所围成的矩形草坪面积为![]() 平方米,试求
平方米,试求![]() 边的长;
边的长;
![]() 按题目的设计要求,________(填“能”或“不能”)围成面积为
按题目的设计要求,________(填“能”或“不能”)围成面积为![]() 平方米的矩形草坪.
平方米的矩形草坪.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com