练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

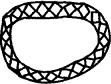
    园林小路，曲径通幽．如图所示，白色正方形石板和青、红两色的三角形石板铺成．问：内圈三角形石板的总数量多，还是外圈三角形石板的总数量多？请说明理由．

    答案：
    解析：

    　　解析：同学们仔细观察图形的结构：容易看出，两个相邻的正方形只有一个顶点重合，它们之间夹着一个外圈的三角形石板与一个内圈的三角形石板．因此内、外圈三角形总个数是相等的．

    　　解：将△ABC绕A点顺时针旋转90°到△AED的位置．则由旋转的特征知道AD＝AC，∠BAC＝∠EAD．又由正方形的性质可知AF＝AC，即得AD＝AF，又由∠EAF＋∠BAC＝180°，可知∠FAD＋∠EAF＝180°，即D、A、F三点在同一条直线上，此时△EDA与△EAF的面积相等．又由于内、外圈三角形石板的个数相等，则内圈三角形石板与外圆三角形石板的总面积相等．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    （1）如图1，以△ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG，连接EG，试判断△ABC与△AEG面积之间的关系，并说明理由．
    （2）园林小路，曲径通幽，如图2所示，小路由白色的正方形理石和黑色的三角形理石铺成．已知中间的所有正方形的面积之和是a平方米，内圈的所有三角形的面积之和是b平方米，这条小路一共占地多少平方米．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图1，以△ABC的边AB、AC为边分别向外作等腰直角△ABD和等腰直角△ACE，连接CD、BE、DE
    （1）证明：△ADC≌△ABE；
    （2）试判断△ABC与△ADE面积之间的关系，并说明理由；
    （3）园林小路，曲径通幽，如图2所示，小路由白色的正方形大理石和黑色的三角形大理石铺成，已知中间的所有正方形的面积之和是a平方米，内圈的所有三角形的面积之和是b平方米，这条小路一共占地
    （a+2b）
    （a+2b）
    平方米．（不用写过程）

    查看答案和解析>>

    科目：初中数学 来源：同步题 题型：解答题

    （1）如图①所示，以△ABC的边AB、AC为边分别向外作正方形ABDE和正方形ACFG，连接EG，试判断△ABC与△AEG面积之间的关系，并说明理由。

                     ①                                  ②
     （2）园林小路，曲径通幽，如图②所示，小路由白色的正方形大理石和黑色的三角形大理石铺成，已知中间的所有正方形的面积之和是a平方米，内圈的所有三角形的面积之和是6平方米，这条小路一共占地多少平方米？

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年安徽铜陵第三中学八年级第二次月考数学试题（带解析） 题型：解答题

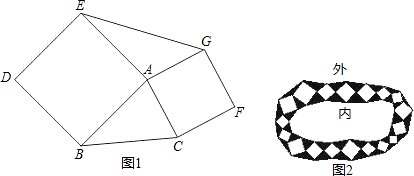
    （1）如图，以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG，试判断△ABC与△AEG面积之间的关系，并说明理由。

    （2）园林小路，曲径通幽，如图2所示，小路由白色的正方形理石和黑色的三角形理石铺成．已知中间的所有正方形的面积之和是a平方米，内圈的所有三角形的面积之和是b平方米，这条小路一共占地多少平方米？

    查看答案和解析>>

    科目：初中数学 来源：2012-2013学年安徽铜陵第三中学八年级第二次月考数学试题（解析版） 题型：解答题

    （1）如图，以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG，试判断△ABC与△AEG面积之间的关系，并说明理由。

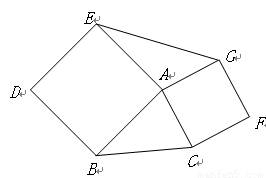
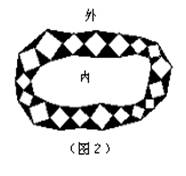
    （2）园林小路，曲径通幽，如图2所示，小路由白色的正方形理石和黑色的三角形理石铺成．已知中间的所有正方形的面积之和是a平方米，内圈的所有三角形的面积之和是b平方米，这条小路一共占地多少平方米？

     

    查看答案和解析>>

    同步练习册答案