
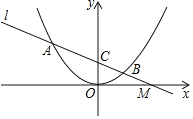
【题目】如图,已知抛物线y=ax2过点A(﹣3,![]() ).
).
(1)求抛物线的解析式;
(2)已知直线l过点A,M(![]() ,0)且与抛物线交于另一点B,与y轴交于点C,求证:MC2=MAMB;
,0)且与抛物线交于另一点B,与y轴交于点C,求证:MC2=MAMB;
(3)若点P,D分别是抛物线与直线l上的动点,以OC为一边且顶点为O,C,P,D的四边形是平行四边形,求所有符合条件的P点坐标.
【答案】(1)y=![]() x2;(2)见解析;(3)P(﹣1﹣
x2;(2)见解析;(3)P(﹣1﹣![]() ,2+
,2+![]() )或(﹣1+
)或(﹣1+![]() ,2﹣
,2﹣![]() )或(﹣2,1).
)或(﹣2,1).
【解析】
(1)利用待定系数法即可解决问题.
(2)构建方程组确定点B的坐标,再利用平行线分线段成比例定理解决问题即可.
(3)如图2中,设P(t,![]() t2),根据PD=CD构建方程求出t即可解决问题.
t2),根据PD=CD构建方程求出t即可解决问题.
解:(1)把点A(﹣3,![]() )代入y=ax2,
)代入y=ax2,
得到![]() =9a,
=9a,
∴a=![]() ,
,
∴抛物线的解析式为y=![]() x2.
x2.
(2)设直线l的解析式为y=kx+b,则有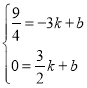 ,
,
解得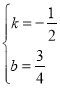 ,
,
∴直线l的解析式为y=﹣![]() x+
x+![]() ,
,
令x=0,得到y=![]() ,
,
∴C(0,![]() ),
),
由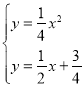 ,解得
,解得![]() 或
或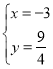 ,
,
∴B(1,![]() ),
),
如图1中,过点A作AA1⊥x轴于A1,过B作BB1⊥x轴于B1,则BB1∥OC∥AA1,
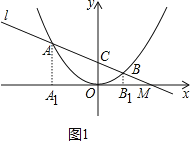
∴![]() =
=![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=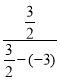 =
=![]() ,
,
∴![]() =
=![]() ,
,
即MC2=MAMB.
(3)如图2中,设P(t,![]() t2)
t2)
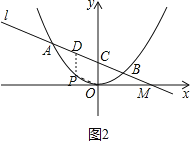
∵OC为一边且顶点为O,C,P,D的四边形是平行四边形,
∴PD∥OC,PD=OC,
∴D(t,﹣![]() t+
t+![]() ),
),
∴|![]() t2﹣(﹣
t2﹣(﹣![]() t+
t+![]() )|=
)|=![]() ,
,
整理得:t2+2t﹣6=0或t2+2t=0,
解得t=﹣1﹣![]() 或﹣1=
或﹣1=![]() 或﹣2或0(舍弃),
或﹣2或0(舍弃),
∴P(﹣1﹣![]() ,2+
,2+![]() )或(﹣1+
)或(﹣1+![]() ,2﹣
,2﹣![]() )或(﹣2,1).
)或(﹣2,1).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在半径为![]() 的
的![]() 中,
中,![]() 是直径,点
是直径,点![]() 是
是![]() 中点,连接
中点,连接![]() ,交
,交![]() 于点
于点![]() ,弦
,弦![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过
,过![]() 的切线
的切线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,![]() .
.
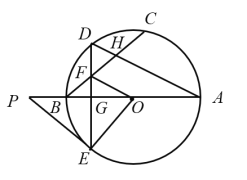
(1)求![]() 的长;
的长;
(2)连接![]() ,求证:
,求证:![]() ;
;
(3)当点![]() 在
在![]() 上运动时,连接
上运动时,连接![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
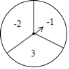
【题目】如图,可以自由转动的转盘被平均分成了三等分标有数字﹣2,3,﹣1的扇形区域转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是3的概率;
(2)转动转盘两次,设第一次得到的数字为x,第二次得到的数字为y,点M的坐标为(x,y),请用树状图或列表法求点M在反比例函数y=﹣![]() 的图象上的概率.
的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂准备今年春季开工前美化厂区,计划对面积为![]() 的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为
的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为![]() 区域的绿化时,甲队比乙队少用6天.
区域的绿化时,甲队比乙队少用6天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少![]() ?
?
(2)若工厂每天需付给甲队的绿化费用为0.4万元,乙队为0.5万元,要使这次的绿化总费用不超过10万元,至少应安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】第5代移动通信技术简称5G,某地已开通5G业务,经测试5G下载速度是4G下载速度的15倍,小明和小强分别用5G与4G下载一部600兆的公益片,小明比小强所用的时间快140秒,求该地4G与5G的下载速度分别是每秒多少兆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y = x2 – 2 m x – 2m – 2与直线y =-x-2 交于C,D两点,将抛物线在C、D两点之间的部分(不含C、D)上恰有两个点的横坐标为整数,则m的取值范围为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=6,DC=2,点P是AB上的动点,则PC+PD的最小值为( )

A.8B.10C.12D.14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中央电视台的“中国诗词大赛”节目文化品位高,内容丰富,某校初二年级模拟开展“中国诗词大赛”比赛,对全年级同学成绩进行统计后分为“优秀”、“良好”、“一般”、“较差”四个等级,并根据成绩绘制成如下两幅不完整的统计图,请结合统计图中的信息,回答下列问题:

(1)扇形统计图中“优秀”所对应的扇形的圆心角为 度,并将条形统计图补充完整.
(2)此次比赛有四名同学活动满分,分别是甲、乙、丙、丁,现从这四名同学中挑选两名同学参加学校举行的“中国诗词大赛”比赛,请用列表法或画树状图法,求出选中的两名同学恰好是甲、丁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】无影塔位于河南汝南城南,俗传冬至正午无塔影,故称无影塔;相传为唐代和尚悟颗所建,故又称“悟颖塔”,该塔应建于北宋中、早期,为豫南地区现存最古之砖塔.某数学小组为了度量塔高进行了如下操作:用一架无人机在距离塔基![]() 8米处垂直起飞30米至点
8米处垂直起飞30米至点![]() 处,测得塔基
处,测得塔基![]() 处的俯角为
处的俯角为![]() ,将无人机沿水平方向向右飞行
,将无人机沿水平方向向右飞行![]() 米至点
米至点![]() ,在此处测得塔顶
,在此处测得塔顶![]() 的俯角为
的俯角为![]() ,请依据题中数据计算无影塔的高度.(结果精确到
,请依据题中数据计算无影塔的高度.(结果精确到![]() ,参考数据:
,参考数据:![]() ,
,![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com