
����Ŀ���ס��������Ⱥ�����������������������ͬ��·�ߵ������240km��ij��.��·��ԭ�׳���ʻ��·��y (km����׳���ʻ��ʱ��x (h���ĺ�����ϵͼ��Ϊ���� O-A-B�� �ҳ���ʻ��·��y (km����׳���ʻ��ʱ��x��h���ĺ�����ϵͼ��Ϊ�߶�CD.
(1)���߶�AB����ֱ�ߵĺ�������ʽ��
(2)���ҳ��ȼ׳������� Сʱ��
���ҳ���������Сʱ���ϼ׳���
(3)�ҳ���������Сʱ��ס����������10ǧ�ף�

���𰸡���1���߶�AB����ֱ�ߵĺ�������ʽΪ![]() ��2����1�����ҳ�����
��2����1�����ҳ�����![]() h���ϼ׳�. ���ҳ�����
h���ϼ׳�. ���ҳ�����![]() Сʱ��
Сʱ��![]() Сʱ��
Сʱ��![]() Сʱ���������10ǧ��.
Сʱ���������10ǧ��.
��������
��1�����ݴ���ϵ����������⣻
��2���������ֱ��CD�Ľ���ʽ���õ�C�����꣬�����ж�����
������ֱ��CD��ֱ��AB����������꼴����⣻
�۸���������ҳ��ϼ׳�֮ǰ���ҳ��ϼ׳�֮���ҳ�û���յ�ʱ���ҳ��ϼ׳�֮���ҳ������յ�ʱ���׳����յ�10km��������ֱ����.
��1����ֱ��AB�ĺ�������ʽΪ��![]() ����A��2��100����B��6��240�������
����A��2��100����B��6��240�������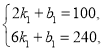
��� 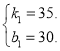
���߶�AB����ֱ�ߵĺ�������ʽΪ![]()
��2������ֱ��CD�ĺ�������ʽΪ��![]() ������2��80����D��4��240�������
������2��80����D��4��240������� 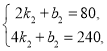
��� 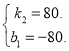
��ֱ��CD�ĺ�������ʽΪ![]()
��C��������1��0��
���ҳ��ȼ׳�������1Сʱ
���1��
������![]()
��� ![]()
��![]() (h)��
(h)��
���ҳ�����![]() h���ϼ׳�.
h���ϼ׳�.
��3���ҳ��ϼ׳�֮ǰ����![]()
���![]()
��![]() (h).
(h).
�ҳ��ϼ׳�֮���ҳ�û���յ�ʱ��
��![]()
![]()
��![]() (h).
(h).
�ҳ��ϼ׳�֮���ҳ������յ�ʱ���׳����յ�10km
��![]() ����
����![]() ����
����![]()
![]()
���ԣ��ҳ�����![]() Сʱ��
Сʱ��![]() Сʱ��
Сʱ��![]() Сʱ���������10ǧ��.
Сʱ���������10ǧ��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,��֪��![]() ,�����²�����ͼ:�ٷֱ���
,�����²�����ͼ:�ٷֱ���![]() ��
��![]() ΪԲ�ģ�����
ΪԲ�ģ�����![]()
![]() �ij�Ϊ�뾶�������������ڵ�
�ij�Ϊ�뾶�������������ڵ�![]() ��
��![]() ������ֱ��
������ֱ��![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ����
����![]() �������н����в�һ���������ǣ� ��
�������н����в�һ���������ǣ� ��
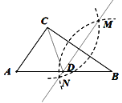
A.![]() B.��
B.��![]() �ǵȱ�������
�ǵȱ�������
C.��D��AB���е�D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ACD�ǡ�ABC����ǣ�BEƽ�֡�ABC��CEƽ�֡�ACD����BE��CE���ڵ�E��
(1)����A=58����E�Ķ�����
(2)�����A���E�Ĺ�ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ĩ����ѩ����С������������Ϸ���ڲ������ϴ���װ��1����ɫ��2����ɫ��ƹ���������������ǻ�ɫ�Ļ�ʤ.С��һ�δӴ�������������С�����ִӴ�������һ����Ȼ����������һ����С�����ȴӴ�������һ����һ����ɫ���ַŻش���ٴӴ�������һ����.��ʱ��С�����ˣ�˵��С�ա�С��ռ�˱��ˣ�����ƽ������Ϊ��Σ� ��.
A. ����ƽ��С�ա�С��ռ������ B. ��ƽ C. ����ƽ��С���Կ��� D. ����ƽ��С��ռ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������������ת�����ɺ졢����ɫ���ɵ�ת�̣�����ת��![]() ����ɫ����ռ����ת�̵�
����ɫ����ռ����ת�̵�![]() ��ת��
��ת��![]() �е���ɫռ����ת�̵�
�е���ɫռ����ת�̵�![]() ��ת��ת�̣�ת��ֹͣ��ָ����ָ��ɫ����ת������ɫ�����ڼס�������������Ϸ��
��ת��ת�̣�ת��ֹͣ��ָ����ָ��ɫ����ת������ɫ�����ڼס�������������Ϸ��
![]() ��ת��ת��
��ת��ת��![]() ����ת��ת��
����ת��ת��![]() ��ÿ��ת��ʮ�Σ�˭ת���ĺ�ɫ������˭��ʤ������Ϊ�����Ϸ��ƽ���������ƽ��˭����ʤ����˵�����ɣ�
��ÿ��ת��ʮ�Σ�˭ת���ĺ�ɫ������˭��ʤ������Ϊ�����Ϸ��ƽ���������ƽ��˭����ʤ����˵�����ɣ�
![]() С���������ĸĽ��������ɵ���������ת�����������ת�̣��������ת�̶�ת���˺�ɫ�����Ӯ��������Ӯ�������С�����һ���������ķ�������д������IJ��裮
С���������ĸĽ��������ɵ���������ת�����������ת�̣��������ת�̶�ת���˺�ɫ�����Ӯ��������Ӯ�������С�����һ���������ķ�������д������IJ��裮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ���������������ȡů���⣬������һ����4000�Ĺܵ���Ϊ��������ʩ���Խ�ͨ��ɵ�Ӱ�죬ʩ��ʱ����������ʵ��ÿ������ܵ�x�ף���ɵ÷���![]() ��20�����ݴ��龰����������������ʾ��ȱʧ������Ӧ��Ϊ��������
��20�����ݴ��龰����������������ʾ��ȱʧ������Ӧ��Ϊ��������
A. ÿ���ԭ�ƻ�������10�ף��������20�����
B. ÿ���ԭ�ƻ�������10�ף��������20�����
C. ÿ���ԭ�ƻ�������10�ף������ǰ20�����
D. ÿ���ԭ�ƻ�������10�ף������ǰ20�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �ı�
�ı�![]() ��
��![]() ���ֽ�����
���ֽ�����![]() ��ͼ����ֱ��
��ͼ����ֱ��![]() �ϣ�������
�ϣ�������![]() �����������ط���������������λ��
�����������ط���������������λ��![]() ʱ�����㣺
ʱ�����㣺
![]()
![]() ����
����![]() ��������·�߳�Ϊ________��
��������·�߳�Ϊ________��
![]() ��
��![]() ������·����ֱ��
������·����ֱ��![]() ��Χ�ɵ����Ϊ________��
��Χ�ɵ����Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
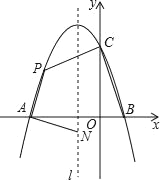
����Ŀ����ͼ��������y=ax2+bx+c��x�ύ�ڵ�A�͵�B��1��0������y�ύ�ڵ�C��0��3������Գ���lΪx=��1��
��1���������ߵĽ���ʽ��д���䶥�����ꣻ
��2��������P�ڵڶ������ڵ��������ϣ�����N�ڶԳ���l�ϣ�
����PA��NA����PA=NAʱ�����ʱ��P�����ꣻ
�����ı���PABC��������ʱ�����ı���PABC��������ֵ����ʱ��P�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com