Question

如图，把矩形纸片ABCD沿EF折叠，使点B落在边AD上的点B'处，点A落在点A'处；
（1）求证：B'E=BF；
（2）设AE=a，AB=b，BF=c，试猜想a，b，c之间的一种关系，并给予证明．

Answer 1

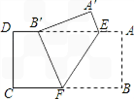
（1）证明：由题意得B'F=BF，∠B'FE=∠BFE，
在矩形ABCD中，AD∥BC，
∴∠B'EF=∠BFE，
∴∠B'FE=∠B'EF，
∴B'F=BE，
∴B'E=BF；
（2）答：a，b，c三者关系不唯一，有两种可能情况：
（i）a，b，c三者存在的关系是a²+b²=c²．
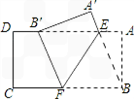
证明：连接BE，则BE=B'E，
由（1）知B'E=BF=c，
∴BE=c．
在△ABE中，∠A=90°，
∴AE²+AB²=BE²，
∵AE=a，AB=b，
∴a²+b²=c²；
（ii）a，b，c三者存在的关系是a+b＞c．
证明：连接BE，则BE=B?E．
由（1）知B'E=BF=c，
∴BE=c，
在△ABE中，AE+AB＞BE，
∴a+b＞c．