
����Ŀ����Ӱ��λ�ں������ϳ��ϣ��״�������������Ӱ���ʳ���Ӱ�����ഫΪ�ƴ�����������������ֳ�����ӱ����������Ӧ���ڱ����С����ڣ�Ϊԥ�ϵ����ִ����֮ש����ij��ѧС��Ϊ�˶������߽��������²�������һ�����˻��ھ�������![]() 8�״���ֱ���30������
8�״���ֱ���30������![]() �����������
�����������![]() ���ĸ���Ϊ
���ĸ���Ϊ![]() �������˻���ˮƽ�������ҷ���
�������˻���ˮƽ�������ҷ���![]() ������
������![]() ���ڴ˴��������
���ڴ˴��������![]() �ĸ���Ϊ
�ĸ���Ϊ![]() ���������������ݼ�����Ӱ���ĸ߶ȣ��������ȷ��
���������������ݼ�����Ӱ���ĸ߶ȣ��������ȷ��![]() ���ο����ݣ�
���ο����ݣ�![]() ��
��![]() ��
��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
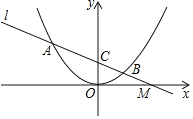
����Ŀ����ͼ����֪������y��ax2����A����3��![]() ����
����
��1���������ߵĽ���ʽ��
��2����ֱ֪��l����A��M��![]() ��0�����������߽�����һ��B����y�ύ�ڵ�C����֤��MC2��MAMB��
��0�����������߽�����һ��B����y�ύ�ڵ�C����֤��MC2��MAMB��
��3������P��D�ֱ�����������ֱ��l�ϵĶ��㣬��OCΪһ���Ҷ���ΪO��C��P��D���ı�����ƽ���ı��Σ������з���������P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() �������ύ�ڵ�
�������ύ�ڵ�![]() ��
��
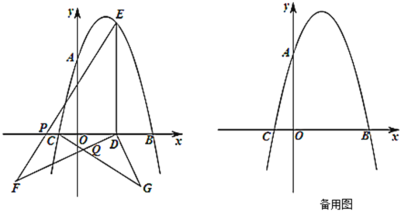
��1���������ߵĽ���ʽ��
��2��![]() Ϊ�߶�
Ϊ�߶�![]() ��һ�㣬��
��һ�㣬��![]() ��
��![]() ��Ĵ��ߣ����������ڵ�
��Ĵ��ߣ����������ڵ�![]() �����߶�
�����߶�![]() ��
��![]() �Ƶ�
�Ƶ�![]() ��ʱ����ת������ͬ�Ľǵ�
��ʱ����ת������ͬ�Ľǵ�![]() ��
��![]() ��λ�ã�ʹ��
��λ�ã�ʹ��![]() ��
��![]() �Ķ�Ӧ��
�Ķ�Ӧ��![]() ��
��![]() ����
����![]() ���·���
���·���![]() ��
��![]() ���ڵ�
���ڵ�![]() ��
��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ʱ�����
ʱ�����![]() �����ꣻ
�����ꣻ
��3��![]() ���������ϣ�
���������ϣ�![]() ������ƽ���ڣ�����
������ƽ���ڣ�����![]() ��
��![]() ��
��![]() ��
��![]() Ϊ������ı���Ϊ����ʱ��ֱ��д����
Ϊ������ı���Ϊ����ʱ��ֱ��д����![]() �����꣮
�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ���ѧ�����ս�������(���˳�ֱ��������Ϊ������)�ָ��һ�������κ�����ȫ�ȵ������Σ���ͼ��ʾ����֪��A=90���� BD=4��CF=6�� ��AO�ij��� �� ��

A.![]() B.
B.![]() C.
C.![]() D.4
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
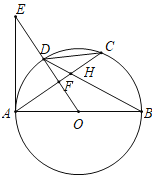
����Ŀ����ͼ��AB��![]() ��ֱ����C��
��ֱ����C��![]() ��һ�㣬D��
��һ�㣬D��![]() ���е㣬
���е㣬![]() Ϊ
Ϊ![]() �ӳ�����һ�㣬AE��
�ӳ�����һ�㣬AE��![]() ��A��AC��BD���ڵ�H����OE���ڵ�F������EC��
��A��AC��BD���ڵ�H����OE���ڵ�F������EC��
��1����֤��EC��![]() �����ߣ�
�����ߣ�
��2����DH=9��![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ij����ҵ�еõ����½����
sin27����sin283���0.122��0.992��0.9945��
sin222����sin268���0.372��0.932��1.0018��
sin229����sin261���0.482��0.872��0.9873��
sin237����sin253���0.602��0.802��1.0000��
sin245����sin245����![]() ��
��![]() ��1.
��1.
�ݴˣ�С�����룺�������������������sin2����sin2(90������)��1.
(1)������30��ʱ����֤sin2����sin2(90������)��1�Ƿ������
(2)С���IJ����Ƿ�������������������֤����������������ٳ�һ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
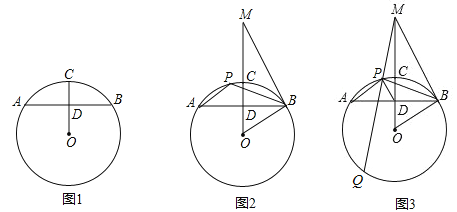
����Ŀ����2017������ʡ�������У���26�⣬10�֣���֪��AB�ǡ�O���ң���C��![]() ���е㣬����OB��OC��OC��AB�ڵ�D��
���е㣬����OB��OC��OC��AB�ڵ�D��
��1����ͼ1����֤��AD=BD��
��2����ͼ2������B����O�����߽�OC���ӳ����ڵ�M����P��![]() ��һ�㣬����AP��BP����֤����APB����OMB=90�㣻
��һ�㣬����AP��BP����֤����APB����OMB=90�㣻
��3����ͼ3���ڣ�2���������£�����DP��MP���ӳ�MP����O�ڵ�Q����MQ=6DP��sin��ABO=![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y��ax2+bx+2��ͼ����x���ཻ�ڵ�A����1��0����B��4��0������y���ཻ�ڵ�C��

��1����ú����ı���ʽ��
��2����PΪ�ú����ڵ�һ�����ڵ�ͼ����һ�㣬����P��PQ��BC������Ϊ��Q������PC��
�����߶�PQ�����ֵ��
�����Ե�P��C��QΪ��������������ABC���ƣ����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
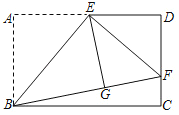
����Ŀ����ͼ������ABCD�У�E��AD���е㣬����ABE��BE�۵�ʹ��A���ڵ�G�����ӳ�BG��CD�ڵ�F������EF����CF��1��DF��2����BC�ij��ǣ��� ����
A.3![]() B.
B.![]() C.5D.2
C.5D.2![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com