已知:k是正整数,直线l1:y=kx+k-1与直线l2:y=(k+1)x+k及x轴围成的三角形的面积为Sk.
(1)求证:无论k取何值,直线l1与l2的交点均为定点;
(2)求S1+S2+S3+…+S2008的值.
分析:(1)根据题意列出方程组,解出x,y的值,即可证出无论k取何值,直线l
1与l
2的交点均为定点.
(2)先求出y=kx+k-1与x轴的交点和y=(k+1)x+k与x轴的交点坐标,再根据三角形面积公式求出S
k,求出S
1=
×(1-
),S
2=
×(
-
),以此类推S
2008=
×(
-
),相加后得到
×(1-
),求出即可.
解答:(1)证明:
解得:
.
∴无论k取何值,直线l
1与l
2的交点均为定点(-1,-1).
(2)解:k≠1时l
1与l
2图象的示意图.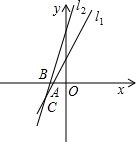
∵y=kx+k-1与x轴的交点为A(
,0),
y=(k+1)x+k与x轴的交点为B(
-,0),
∴S
K=S
△ABC=
×AB×
=
×
×1=
k=1时结论同样成立.
∴S
1+S
2+S
3+…+S
2008的
=
[
+
+…
]
=
[(1-
)+(
-
)+…+(
-)]
=
×(1-
)
=
×
=
.
点评:此题考查了一次函数的综合题;解题的关键是一次函数的图象与两坐标轴的交点坐标特点,与x轴的交点的纵坐标为0,与y轴的交点的横坐标为0.



