
【题目】如图,在正方形![]() 中,
中,![]() 是边
是边![]() 上的动点(与点
上的动点(与点![]() 、
、![]() 不重合),且
不重合),且![]() ,
,![]() 于点
于点![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 、
、![]() .
.
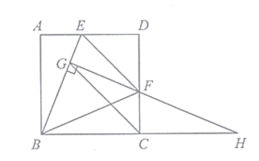
(1)求证:①![]()
![]()
![]() ;②
;②![]() ;
;
(2)若![]() ,在点
,在点![]() 运动过程中,探究:
运动过程中,探究:
①线段![]() 的长度是否改变?若不变,求出这个定值;若改变,请说明理由;
的长度是否改变?若不变,求出这个定值;若改变,请说明理由;
②当![]() 为何值时,
为何值时,![]() 为等腰直角三角形.
为等腰直角三角形.
【答案】(1)①见解析;②见解析;(2)①在点![]() 运动过程中,
运动过程中,![]() 的长度不变,且CG=2;②AE=
的长度不变,且CG=2;②AE=![]() .
.
【解析】
(1)①由题意易得△DEF是等腰直角三角形,即得DE=DF,然后根据正方形的性质和SAS即可证得结论;
②根据全等三角形的性质可得![]() ,根据余角的性质可得
,根据余角的性质可得![]() ,从而可得
,从而可得![]() ,于是可得结论;
,于是可得结论;
(2)①由![]() 、
、![]() 可得
可得![]() ,然后根据直角三角形斜边中线的性质即得结论;
,然后根据直角三角形斜边中线的性质即得结论;
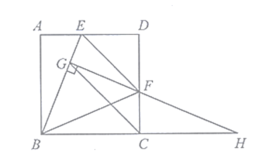
②解法一:如图1,延长![]() 交
交![]() 于点
于点![]() ,易证
,易证![]() 是等腰直角三角形,即
是等腰直角三角形,即![]() ,设
,设![]() ,则
,则![]() ,由
,由![]() 为等腰直角三角形可得
为等腰直角三角形可得![]() ,进而可得
,进而可得![]() ,由
,由![]() 即可求出x的值,即为AE的值;
即可求出x的值,即为AE的值;
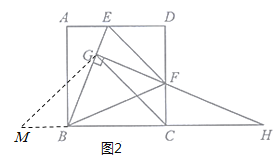
解法二:如图2,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,根据AAS易证
,根据AAS易证![]()
![]()
![]() ,所以
,所以![]() ,
,![]() ,从而可得
,从而可得![]() 是等腰直角三角形,由CG=2可得MC的长,进而可得MB的长,即为AE的长;
是等腰直角三角形,由CG=2可得MC的长,进而可得MB的长,即为AE的长;
解法三:如图3,过点![]() 作
作![]() 于点
于点![]() ,由B、C、F、G四点共圆可得∠BCG=∠BFG=45°,从而可得
,由B、C、F、G四点共圆可得∠BCG=∠BFG=45°,从而可得![]() 是等腰直角三角形,可得
是等腰直角三角形,可得![]() ,进而可得NH的长,由
,进而可得NH的长,由![]() 即可求出FC,即为AE的长.
即可求出FC,即为AE的长.
(1)证明:①∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴△![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]() ;
;
②∵![]()
![]()
![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;

(2)①在点![]() 运动过程中,
运动过程中,![]() 的长度不变.
的长度不变.
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() (定值);
(定值);
②解法一:如图1,延长![]() 交
交![]() 于点
于点![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() 是等腰直角三角形,即
是等腰直角三角形,即![]() .
.
设![]() ,则
,则![]() .
.
∵![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
在等腰![]() 中,∵
中,∵![]() ,∴
,∴![]() .
.
解得:![]() ,即
,即![]() .
.

②解法二:如图2,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,则∠MGB=∠CGF,
,则∠MGB=∠CGF,
∵∠M+∠MCG=90°,∠GCF+∠MCG=90°,
∴∠M=∠GCF,
又∵GB=GF,
∴![]()
![]()
![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]()
![]() ,
,
∴![]() ,
,
∴![]() .
.
②解法三:如图3,过点![]() 作
作![]() 于点
于点![]() ,
,
∵∠BGF+∠BCF=180°,
∴B、C、F、G四点共圆,
∴∠BCG=∠BFG=45°,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
∴![]() ,
,
∴![]() .
.
∵![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() .
.



 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】某软件开发公司开发了A、B两种软件,每种软件成本均为1400元,售价分别为2000元、1800元,这两种软件每天的销售额共为112000元,总利润为28000元.
(1)该店每天销售这两种软件共多少个?
(2)根据市场行情,公司拟对A种软件降价销售,同时提高B种软件价格.此时发现,A种软件每降50元可多卖1件,B种软件每提高50元就少卖1件.如果这两种软件每天销售总件数不变,那么这两种软件一天的总利润最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA,PB,AB,已知∠PBA=∠C.

(1)求证:PB是⊙O的切线;
(2)连接OP,若OP∥BC,且OP=8,⊙O的半径为![]() ,求BC的长.
,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径长为1,AB、AC是⊙O的两条弦,且AB=AC,BO的延长线交AC于点D,连接OA、OC.
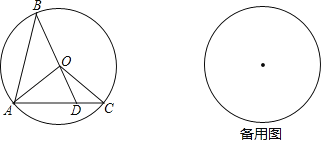
(1)求证:△OAD∽△ABD;
(2)当△OCD是直角三角形时,求B、C两点的距离;
(3)记△AOB、△AOD、△COD的面积分别为S1、S2、S3,如果S22=S1S3,试证明点D为线段AC的黄金分割点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M,N是以AB为直径的⊙O上的点,且![]() =
=![]() ,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
,弦MN交AB于点C,BM平分∠ABD,MF⊥BD于点F.
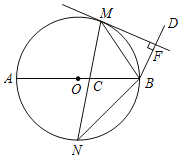
(1)求证:MF是⊙O的切线;
(2)若CN=3,BN=4,求CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在锐角![]() 中,
中,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按逆时针方向旋转,得到
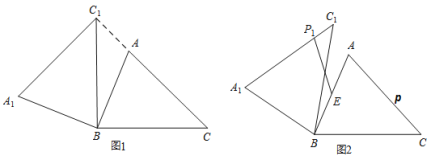
按逆时针方向旋转,得到![]() .(1)如图1,当点
.(1)如图1,当点![]() 在线段
在线段![]() 的延长线上时,则
的延长线上时,则![]() 的度数为______________度;(2)如图2,点
的度数为______________度;(2)如图2,点![]() 为线段
为线段![]() 中点,点
中点,点![]() 是线段
是线段![]() 上的动点,在
上的动点,在![]() 绕点
绕点![]() 按逆时针方向旋转过程中,点
按逆时针方向旋转过程中,点![]() 的对应点是点
的对应点是点![]() ,则线段
,则线段![]() 长度最小值是_____________.
长度最小值是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上运动(不与点
上运动(不与点![]() ,
,![]() 重合),以
重合),以![]() 为边作正方形
为边作正方形![]() ,使点
,使点![]() 在正方形
在正方形![]() 内,连接
内,连接![]() ,则下列结论:①
,则下列结论:①![]() ;②当
;②当![]() 时,
时,![]() ;③点
;③点![]() 到直线
到直线![]() 的距离为
的距离为![]() ;④
;④![]() 面积的最大值是
面积的最大值是![]() .其中正确的结论是______.(填写所有正确结论的序号)
.其中正确的结论是______.(填写所有正确结论的序号)

查看答案和解析>>
科目:初中数学 来源: 题型:
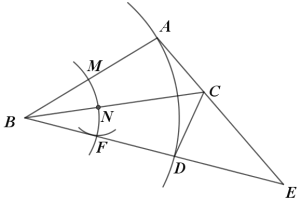
【题目】如图所示,在△ABC中,按以下步骤作图:①以点B为圆心,任意长为半径作弧,分别交BA、BC于点M、N;再以点N为圆心,MN长为半径作弧交前面的弧于点F,作射线BF交AC的延长线于点E.
②以点B为圆心,BA长为半径作弧交BE于点D,连接CD.
请你观察图形,解答下列问题:
(1)求证:△ABC≌△DBC;
(2)若∠A=100°,∠E=50°,求∠ACB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com