
【题目】如图,直线AB:y=一 ![]() x+2与x轴相交于点A,与y轴交于点B.直线CD:y=kx+b经过点c(一1,0),D(0,
x+2与x轴相交于点A,与y轴交于点B.直线CD:y=kx+b经过点c(一1,0),D(0, ![]() ),与直线AB交于点E.
),与直线AB交于点E.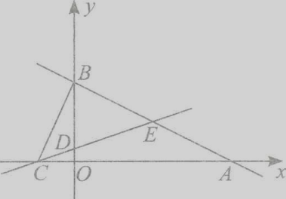
(1)求直线CD的函数关系式;
(2)连接BC,求△BCE的面积;
(3)设点Q的坐标为(m,2),求m的值使得QA+QE值最小.
【答案】
(1)解:设直线 ![]() 表达式为:
表达式为: ![]()
由题意得: 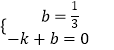
∴ ![]()
∴直线 ![]() 表达式为:
表达式为: ![]()
(2)解:∵ 
∴ ![]() , ∴E(2,1),
, ∴E(2,1),
∵C(-1,0),A(4,0),
∴A C=5, OB=2, ![]()
∴ ![]()
![]()
![]()
![]()
(3)解:点 ![]() 关于直线
关于直线 ![]() 的对称点为
的对称点为 ![]() ,连接
,连接 ![]() 交直线
交直线 ![]() 于点
于点 ![]() ,则点
,则点 ![]() 即为所求的点
即为所求的点

设直线 ![]() 表达式为:
表达式为: ![]()
由题意得: ![]()
∴ ![]()
∴ ![]()
∵ ![]() ∴
∴ ![]() ∴
∴ ![]() ∴
∴ ![]()
∴m= ![]()
【解析】(1)设直线 C D 表达式为: y = k x + b,用待定系数法即可求出直线CD的解析式 ;
(2)首先解直线AB与直线CD的解析式联立的方程组求出E点的坐标,根据A,B,C,E四点的坐标得出AC,OB的长,及E点到y轴的距离,根据 S Δ B C E = S Δ A B C S Δ A C E带值计算即可;
(3) E 关于直线 y = 2 的对称点为 E’ ( 2 , 3 ) ,连接 A E’交直线 y = 2 于点 Q ,则点 Q 即为所求的点,用待定系数法求出直线 A E’的解析式,然后把y=2代入直线 A E’的解析式求出对应的x的值,从而得出Q点的坐标,得到m的值。


科目:初中数学 来源: 题型:
【题目】用甲、乙两种原料配制某种饮料,这两种原料的维生素C含量及购买两种原料的价格如表:
原料 | 甲 | 乙 |
维生素C的含量/(单位/kg) | 600 | 100 |
原料价格/(元/kg) | 8 | 4 |
现配制这种饮料10千克,要求至少含有4200单位的维生素C,且购买甲、乙两种原料的费用不超过72元,求所需甲种原料的质量应满足的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中是假命题的是( )
A. 平面内,垂直于同一条直线的两条直线平行;
B. 同旁内角互补;
C. 等角的余角相等;
D. 互为补角的两个角不都是锐角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一条长400米的直线跑道上同起点、同终点、同方向匀速跑步,先到终点的人原地休息.已知甲先出发3秒,在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,则下列结论正确的个数有( )
①乙的速度是4米/秒;
②离开起点后,甲、乙两人第一次相遇时,距离起点12米;
③甲从起点到终点共用时83秒;
④乙到达终点时,甲、乙两人相距68米;
⑤乙离开起点12秒后,甲乙第一次相遇.
A.4个
B.3个’
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与反比例函数
,与反比例函数![]() 的图象交于点
的图象交于点![]() .
.
(![]() )
)![]() __________;
__________;![]() __________.
__________.
(![]() )点
)点![]() 是直线
是直线![]() 上的动点(与点
上的动点(与点![]() ,
,![]() 不重合),过点
不重合),过点![]() 且平行于
且平行于![]() 轴的直线
轴的直线![]() 交这个反比例函数的图象于点
交这个反比例函数的图象于点![]() ,当点
,当点![]() 的横坐标为
的横坐标为![]() 时,得
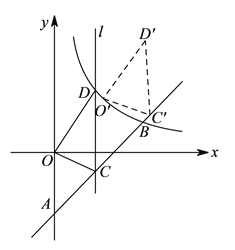
时,得![]() ,现将
,现将![]() 沿射线
沿射线![]() 方向平移一定的距离(如图),得到
方向平移一定的距离(如图),得到![]() ,若点
,若点![]() 的对应点
的对应点![]() 落在该反比例函数图象上,求点
落在该反比例函数图象上,求点![]() ,
,![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
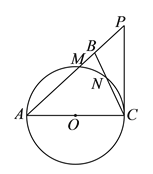
【题目】如图,在![]() 中,
中,![]() ,以
,以![]() 为直径的⊙
为直径的⊙![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,点
,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .
.
(![]() )求证:直线
)求证:直线![]() 是⊙
是⊙![]() 的切线.
的切线.
(![]() )若
)若![]() ,
,![]() ,求点
,求点![]() 到
到![]() 的距离.
的距离.
(![]() )在第(
)在第(![]() )的条件下,求
)的条件下,求![]() 的周长.
的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作⊙O的切线交AC于点D,且ED⊥AC.


(1)试判断△ABC的形状,并说明理由;
(2)如图2,若线段AB、DE的延长线交于点F,∠C=75°,CD=![]() ,求⊙O的半径和BF的长
,求⊙O的半径和BF的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com