【题目】已知一次函数
（
，
是常数，
）的图象过
，
两点.
（1）在图中画出该一次函数并求其表达式；
（2）若点
在该一次函数图象上，求
的值；
（3）把的图象向下平移3个单位后得到新的一次函数图象，在图中画出新函数图形，并直接写出新函数图象对应的表达式.
科目：初中数学 来源： 题型：
【题目】如图：梯形ABCD中，AD∥BC，∠ABC=90°，AD=4， AB=3，
，在线段BC上取一点P（不与B、C重合），联结DP，作射线PQ⊥DP，PQ与直线AB交于点Q．
（1）求出梯形ABCD的面积；
（2）若点Q在边AB上，设CP=x，AQ=y，试写出y关于自变量x的函数关系式，并写出定义域．
（3）△DPC是等腰三角形，求AQ的长．
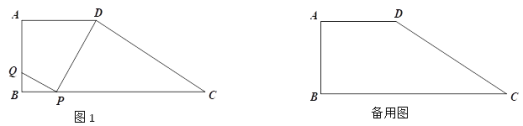
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，直线
为一、三象限角平分线．点P关于y轴的对称点称为P的一次反射点，记作
；关于直线的对称点称为点P的二次反射点，记作
．例如，点
的一次反射点为
，二次反射点为
．根据定义，回答下列问题：
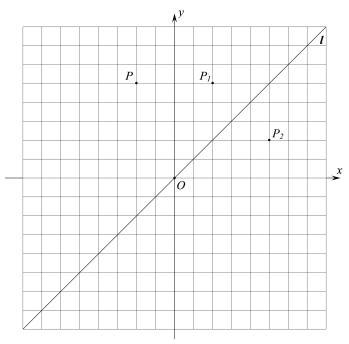
（1）点的一次反射点为________，二次反射点为__________；
（2）当点A在第一象限时，点
，
，
中可以是点A的二次反射点的是_________；
（3）若点A在第二象限，点
，
分别是点A的一次、二次反射点，△
为等边三角形，求射线OA与x轴所夹锐角的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在等边
中，点
是边
上一点.作射线
，点
关于射线的对称点为点
.连接
并延长，交射线于点
.
（1）如图，连接
，
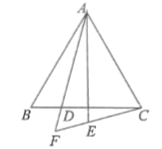
①与
的数量关系是__________；
②设
，用
表示
的大小；
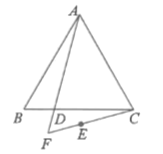
（2）如图，用等式表示线段
，
，
之间的数量关系，并证明.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们知道，演绎推理的过程称为证明，证明的出发点和依据是基本事实.证明三角形全等的基本事实有：两边及其夹角分别相等的两个三角形全等，两角及其夹边分别相等的两个三角形全等，三边分别相等的两个三角形全等.
（1）请选择利用以上基本事实和三角形内角和定理，结合下列图形，证明：两角分别相等且其中一组等角的对边相等的两个三角形全等.
（2）把三角形的三条边和三个角统称为三角形的六个元素.如果两个三角形有四对对应元素相等，这两个三角形一定全等吗？请说明理由.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等边
外有一点
，连接
，
，
.
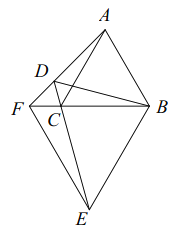
图1 图2 图3
（1）如图1，若
，求证：
平分
；
（2）如图2，若
，求证：
；
（3）如图3，延长
交
的延长线于点
，以
为边向下作等边
，若点，
，
在同一直线上，且
，直接写出
的度数为___________（结果用含
的式子表示）.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD与正方形A1B1C1D1关于某点中心对称，已知A, D1,D三点的坐标分别是（0,4），（0，3），（0，2）.
(1)对称中心的坐标；
(2)写出顶点B, C, B1 , C1的坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“丹棱冻粑”是眉山著名特色小吃，产品畅销省内外，现有一个产品销售点在经销时发现：如果每箱产品盈利10元，每天可售出50箱；若每箱产品涨价1元，日销售量将减少2箱．
（1）现该销售点每天盈利600元，同时又要顾客得到实惠，那么每箱产品应涨价多少元？
（2）若该销售点单纯从经济角度考虑，每箱产品应涨价多少元才能获利最高？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
