
【题目】已知,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,D是AC边上的一个动点,将
,D是AC边上的一个动点,将![]() 沿BD所在直线折叠,使点A落在点E处.
沿BD所在直线折叠,使点A落在点E处.
![]() 如图
如图![]() ,若点D是AC的中点,连接
,若点D是AC的中点,连接![]() 求证:四边形BCED是平行四边形;
求证:四边形BCED是平行四边形;
![]() 如图
如图![]() ,若
,若![]() ,求
,求![]() 的值.
的值.


【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)根据直角三角形的性质得到AD=CD=4=BC,根据翻转变换的性质得到DE=AD=4,∠EDB=∠ADB=135°,根据平行四边形的判定定理证明;
(2)连接AE,分别过点D作DF⊥AB于点F,过点E作EM⊥AC于点M,作EN⊥BC,交BC的延长线于点N,延长BD交AE于点G,根据勾股定理分别求出BD、AB,根据正弦的定义计算即可.
![]() 证明:在
证明:在![]() 中,
中,![]() ,
,![]() ,点D是AC的中点,
,点D是AC的中点,
![]() ,
,
![]() 是等腰直角三角形,
是等腰直角三角形,
![]() ,
,![]() ,
,
由折叠得:![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,又
,又![]() ,
,
![]() 四边形BCED是平行四边形;
四边形BCED是平行四边形;
![]() 解:如图
解:如图![]() ,连接AE,分别过点D作
,连接AE,分别过点D作![]() 于点F,过点E作
于点F,过点E作![]() 于点M,
于点M,
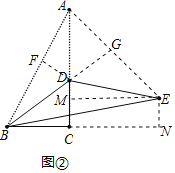
作![]() ,交BC的延长线于点N,延长BD交AE于点G,
,交BC的延长线于点N,延长BD交AE于点G,
则![]() 为等腰三角形,
为等腰三角形,![]() ,
,
设![]() ,则
,则![]() ,
,
在![]() 中,由勾股定理得:
中,由勾股定理得:![]() ,
,
![]() ,
,
![]() ,即
,即![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
由![]() ∽
∽![]() ,可得
,可得![]() ,
,
![]()
![]() ,又
,又![]() ,
,![]() .
.
![]() ,
,
由![]() ∽
∽![]() ,可得
,可得![]()
![]() ,
,
![]() ,
,
![]() 四边形EMCN是矩形,
四边形EMCN是矩形,
![]() 又
又![]()
![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
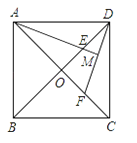
【题目】(8分)如图,在正方形ABCD中,对角线AC、BD相交于O,E、F分别在OD、OC上,且DE=CF,连结DF、AE,AE的延长线交于DF于点M,求证:AM⊥DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点 E.

(1)求证:DE=CE.
(2)若∠CDE=25°,求∠A 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC=5,线段AB的垂直平分线DE分别交边AB、AC于点E、D.

(1)若∠A=40°,求∠DBC的度数;
(2)若△BCD的周长为8,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,该校有几种购买方案?
(3)上面的哪种方案费用最低?按费用最低方案购买需要多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强学生的安全意识,某校组织了学生参加安全知识竞赛,从中抽取了部分学生成绩(得分数取正整数,满分为![]() 分)进行统计,绘制统计图如下(未全完成),已知
分)进行统计,绘制统计图如下(未全完成),已知![]() 组的频数比
组的频数比![]() 组小
组小![]() ,解答下列问题:
,解答下列问题:

(1)求样本容量及频数分布直方图中的![]() ,
,![]() 的值;
的值;
(2)扇形统计图中,![]() 部分所对的圆心角为
部分所对的圆心角为![]() ,求
,求![]() 的值并补全频数分布直方图;
的值并补全频数分布直方图;
(3)若成绩在![]() 分以上优秀,全校共有
分以上优秀,全校共有![]() 名学生估计成绩优秀的学生有多少名?
名学生估计成绩优秀的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
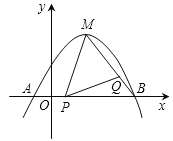
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() 两点,与x轴交于另一点B.
两点,与x轴交于另一点B.
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 若抛物线的顶点为M,点P为线段OB上一动点
若抛物线的顶点为M,点P为线段OB上一动点![]() 不与点B重合
不与点B重合![]() ,点Q在线段MB上移动,且
,点Q在线段MB上移动,且![]() ,设线段
,设线段![]() ,
,![]() ,求
,求![]() 与x的函数关系式,并直接写出自变量x的取值范围;
与x的函数关系式,并直接写出自变量x的取值范围;
![]() 在同一平面直角坐标系中,两条直线
在同一平面直角坐标系中,两条直线![]() ,
,![]() 分别与抛物线交于点E、G,与
分别与抛物线交于点E、G,与![]() 中的函数图象交于点F、
中的函数图象交于点F、![]() 问四边形EFHG能否成为平行四边形?若能,求m、n之间的数量关系;若不能,请说明理由.
问四边形EFHG能否成为平行四边形?若能,求m、n之间的数量关系;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农夫将苹果树种在正方形的果园内,为了保护苹果树不受风吹,他在苹果树的周围种上针叶树.在下图里,你可以看到农夫所种植苹果树的列数(n)和苹果树数量及针叶树数量的规律:当n为某一个数值时,苹果树数量会等于针叶树数量,则n为( )

A. 6 B. 8 C. 12 D. 16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com