
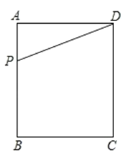
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上的一动点,连结
上的一动点,连结![]() .
.
(1)若将![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在矩形的对角线上点
落在矩形的对角线上点![]() 处,试求
处,试求![]() 的长;
的长;
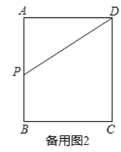
(2)点![]() 运动到某一时刻,过点
运动到某一时刻,过点![]() 作直线
作直线![]() 交
交![]() 于点
于点![]() ,将
,将![]() 与
与![]() 分别沿
分别沿![]() 与
与![]() 折叠,点
折叠,点![]() 与点
与点![]() 分别落在点
分别落在点![]() ,
,![]() 处,若
处,若![]() ,
,![]() ,
,![]() 三点恰好在同一直线上,且
三点恰好在同一直线上,且![]() 试求此时
试求此时![]() 的长;
的长;
(3)当点![]() 运动到边
运动到边![]() 的中点处时,过点
的中点处时,过点![]() 作直线
作直线![]() 交
交![]() 于点
于点![]() ,将
,将![]() 与
与![]() 分别沿
分别沿![]() 与
与![]() 折叠,点
折叠,点![]() 与点
与点![]() 重合于点
重合于点![]() 处,连结
处,连结![]() ,请求出
,请求出![]() 的长.
的长.

【答案】(1)![]() 的长为
的长为![]() 或
或![]() ;(2)
;(2)![]() 的长为1或3;(3)
的长为1或3;(3)![]() .
.
【解析】
(1)分两种情形:①当点A落在对角线BD上时,设AP=PA′=x,构建方程即可解决问题;②当点A落在对角线AC上时,利用相似三角形的性质构建方程即可解决问题;
(2)分两种情形分别求解即可解决问题;
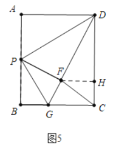
(3)如图5中,作FH⊥CD由H.想办法求出FH、CH即可解决问题;
(1)①当点![]() 落在对角线
落在对角线![]() 上时,设
上时,设![]() ,
,
在![]() ,∵
,∵![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
在![]() 中,
中,![]() ,解得
,解得![]() ,
,
∴![]() .
.
②当点![]() 落在对角线
落在对角线![]() 上时,
上时,
由翻折性质可知:![]() ,则有
,则有![]() ,
,
∴![]() ,∴
,∴![]() .
.
∴![]() 的长为
的长为![]() 或
或![]() ;
;
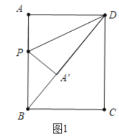
(2)①如图3中,设![]() ,则
,则![]() ,
,
根据折叠的性质可知:![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() ;
;
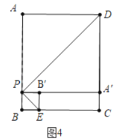
②如图4中,设![]() ,则
,则![]() ,
,
根据折叠的性质可知:![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ;
;
综上所述,![]() 的长为1或3;
的长为1或3;
(3)如图5中,作![]() 由
由![]() .
.
由翻折的性质可知;![]() .
.![]() ,
,![]() 共线,
共线,
设![]() ,在
,在![]() 中,
中,![]() ,
,
解得![]() ,∴
,∴![]() ,
,![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴ ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
在![]() 中,
中, .
.




 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.
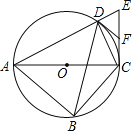
(1)求∠CDE的度数;
(2)求证:DF是⊙O的切线;
(3)若AC=2![]() DE,求tan∠ABD的值.
DE,求tan∠ABD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于_____.
[Failed to download image : http://qbm-images.oss-cn-hangzhou.aliyuncs.com/QBM/2018/4/13/1923101670465536/1923902127538176/STEM/3534c7f6f1a5489684ae6308493b71da.png]
查看答案和解析>>
科目:初中数学 来源: 题型:
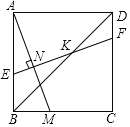
【题目】如图,已知正方形ABCD的边长为1,点M是BC边上的动点(不与B,C重合),点N是AM的中点,过点N作EF⊥AM,分别交AB,BD,CD于点E,K,F,设BM=x.
(1)AE的长为______(用含x的代数式表示);
(2)设EK=2KF,则![]() 的值为______.
的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
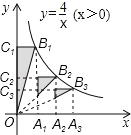
【题目】如图,点A1、A2、A3在x轴上,且OA1=A1A2=A2A3,分别过点A1、A2、A3作y轴的平行线,与反比例函数![]() 的图象分别交于点B1、B2、B3,分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3,连结OB1、OB2、OB3,那么图中阴影部分的面积之和为 .
的图象分别交于点B1、B2、B3,分别过点B1、B2、B3作x轴的平行线,分别与y轴交于点C1、C2、C3,连结OB1、OB2、OB3,那么图中阴影部分的面积之和为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).

请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
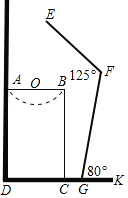
【题目】如图是小米洗漱时的侧面示意图.洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小米身高160cm,下半身FG=100cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台距离GC=15cm(点D,C,G,K在同一直线上).
(1)此时小米头部E点与地面DK相距多少?
(2)若小米的头部E恰好在洗漱盆AB的中点O的正上方,她应向前或向后移动多少厘米?(sin80°≈0.98,cos80°≈0.18,![]() ≈1.41,结果精确到0.1)
≈1.41,结果精确到0.1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-2mx+m2+3(m是常数).
(1)求证:不论m为何值,该函数的图象与x轴没有公共点;
(2)把该函数的图象沿y轴向下平移多少个单位长度后,得到的函数的图象与x轴只有一个公共点?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com