
【题目】对于平面直角坐标系![]() 中的图形
中的图形![]() ,
,![]() ,给出如下定义:
,给出如下定义:![]() 为图形
为图形![]() 上任意一点,
上任意一点,![]() 为图形
为图形![]() 上任意一点,如果线段
上任意一点,如果线段![]() 的长度有最小值,那么称这个最小值为图形
的长度有最小值,那么称这个最小值为图形![]() ,
,![]() 的“近距”,记作
的“近距”,记作![]() ;如果线段
;如果线段![]() 的长度有最大值,那么称这个最大值为图形
的长度有最大值,那么称这个最大值为图形![]() ,
,![]() 的“远距”,记作
的“远距”,记作![]() .
.
已知点![]() ,
,![]() .
.
(1)![]() (点
(点![]() ,线段
,线段![]() )
)![]() ______,
______,![]() (点
(点![]() ,线段
,线段![]() )
)![]() ______;
______;
(2)一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() (线段
(线段![]() ,线段
,线段![]() )
)![]() ,
,
①求![]() 的值;
的值;
②直接写出![]() (线段
(线段![]() ,线段
,线段![]() )
)![]() ______;
______;
(3)![]() 的圆心为
的圆心为![]() ,半径为1.若
,半径为1.若![]() (
(![]() 线段
线段![]() )
)![]() ,请直接写出
,请直接写出![]() (
(![]() ,线段
,线段![]() )的取值范围.
)的取值范围.
【答案】(1)3,5;(2)①![]() ; ②
; ②![]() ;(3)
;(3)![]() (
(![]() ,线段
,线段![]() )
)![]() .
.
【解析】
(1)由图可知O到A的距离最小,O到B的距离最大,求出相应距离即可;、
(2)根据题意判断![]() 为等腰直角三角形,可得
为等腰直角三角形,可得![]() ,得到OC=OD,求得点C坐标,从而得到k的值;根据线段CD与线段AB的位置关系,得到BC间距离即为所求;
,得到OC=OD,求得点C坐标,从而得到k的值;根据线段CD与线段AB的位置关系,得到BC间距离即为所求;
(3)通过对![]() 在
在![]() 轴上的位置的讨论,即可得到
轴上的位置的讨论,即可得到![]() (
(![]() ,线段
,线段![]() )的取值范围
)的取值范围
(1)作图如下:
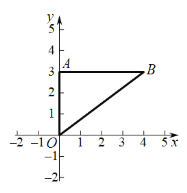
A(0,3),B(4,3)
∴OA=3,AB=4
∴点O到线段AB上的点A的距离最短,OA=3;
∴点O到线段AB上的点B的距离最大,![]() ;
;
(2)①过点A作![]() 于点E,
于点E,
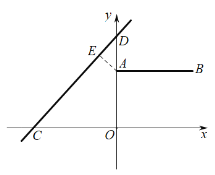
则![]() (线段
(线段![]() ,线段
,线段![]() )
)![]() ,
,
![]() 直线
直线![]() 与y轴交点为
与y轴交点为![]() ,
,
与x轴交点C在x轴负半轴,
![]() .
.
![]() .
.
![]() .
.
![]() 点C的坐标为
点C的坐标为![]() .
.
![]() .
.
②由图可知,线段CD上一点,到线段AB上一点的距离的最大值为BC的长度,作图如下:
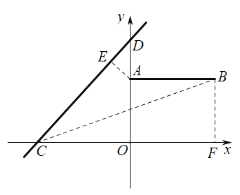
∴![]()
故答案为:![]()
(3)作图如下:
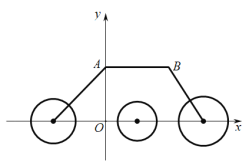
若![]() 在点A的左侧,则
在点A的左侧,则![]() ,
,![]() ,则
,则![]() ,即T(
,即T(![]() )
)
此时![]() (
(![]() ,线段
,线段![]() )=
)=![]()
若![]() 在点AB中间,当圆心T为AB中垂线与
在点AB中间,当圆心T为AB中垂线与![]() 轴交点,即T(
轴交点,即T(![]() ),
),
此时![]() (
(![]() ,线段
,线段![]() )最小,即
)最小,即![]() (
(![]() ,线段
,线段![]() )=
)=![]()
故答案为:![]() (
(![]() ,线段
,线段![]() )
)![]() .
.


科目:初中数学 来源: 题型:
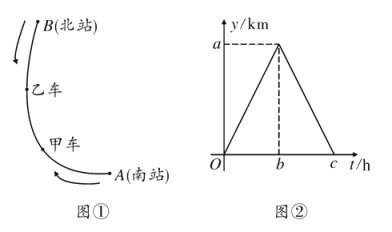
【题目】如图①,长为120 km的某段线路AB上有甲、乙两车,分别从南站A和北站B同时出发相向而行,到达B,A后立刻返回到出发站停止,速度均为40 km/h,设甲车,乙车距南站A的路程分别为y甲,y乙(km),行驶时间为t(h).
(1)图②已画出y甲与t的函数图象,其中a=____,b=____,c=____;
(2)分别写出0≤t≤3及3<t≤6时,y乙与时间t之间的函数关系式;
(3)在图②中补画y乙与t之间的函数图象,并观察图象计算出在整个行驶过程中两车相遇的次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
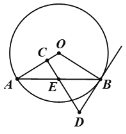
【题目】如图,AB是⊙O的弦,过AB的中点E作EC⊥OA于C,过点B作⊙O的切线BD交CE的延长线于点D.
(1)求证:DB=DE;
(2)连接AD,若AB=24,DB=10,求四边形OADB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
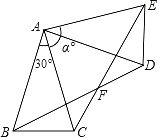
【题目】如图,△ABC中,AB=AC,∠BAC=30°,将△ABC绕点A按逆时针方向旋转α°.得到△ADE,连接BD,CE交于点F.
(1)求证:△ABD≌△ACE;
(2)用α表示∠ACE的度数;
(3)若使四边形ABFE是菱形,求α的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
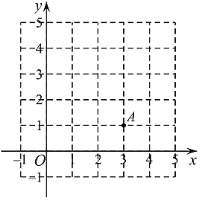
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象
的图象![]() 经过点
经过点![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值及点
的值及点![]() 的坐标;
的坐标;
(2)直线![]() 与函数
与函数![]() 的图象
的图象![]() 交于点
交于点![]() ,记图象
,记图象![]() 在点
在点![]() ,
,![]() 之间的部分与线段
之间的部分与线段![]() ,
,![]() ,
,![]() 围成的区域(不含边界)为
围成的区域(不含边界)为![]() .
.
①当![]() 时,直接写出区域
时,直接写出区域![]() 内的整点个数;
内的整点个数;
②若区域![]() 内恰有2个整点,结合函数图象,求
内恰有2个整点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
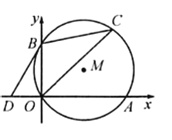
【题目】在平面直角坐标系中,⊙M过坐标原点O且分别交x轴、y轴于点A,B,点C为第一象限内⊙M上一点.若点A(6,0),∠BCO=30°.
(1)求点B的坐标;
(2)若点D的坐标为(-2,0),试猜想直线DB与⊙M的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果![]() 都是非零整数,且
都是非零整数,且![]() ,那么就称
,那么就称![]() 是“4倍数”.
是“4倍数”.
(1)30到35之间的“4倍数”是_________,小明说:![]() 是“4倍数”,嘉淇说:
是“4倍数”,嘉淇说:![]() 也是“4倍数”,他们谁说的对?____________.
也是“4倍数”,他们谁说的对?____________.
(2)设![]() 是不为零的整数.
是不为零的整数.
①![]() 是___________的倍数;
是___________的倍数;
②任意两个连续的“4倍数”的积可表示为____________,它_____________(填“是”或“不是”)32的倍数.
(3)设三个连续偶数的中间一个数是![]() (
(![]() 是整数),写出它们的平方和,并说明它们的平方和是“4倍数”.
是整数),写出它们的平方和,并说明它们的平方和是“4倍数”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是以O为圆心,AB长为直径的半圆弧,点C是AB上一定点.点P是
是以O为圆心,AB长为直径的半圆弧,点C是AB上一定点.点P是![]() 上一动点,连接PA,PC,过点P作PD⊥AB于D.已知AB=6cm,设A、P两点间的距离为x cm,P、C两点间的距离为y1 cm,P、D两点间的距离为y2 cm.
上一动点,连接PA,PC,过点P作PD⊥AB于D.已知AB=6cm,设A、P两点间的距离为x cm,P、C两点间的距离为y1 cm,P、D两点间的距离为y2 cm.
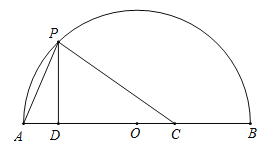
小刚根据学习函数的经验,分别对函数y1和y2随自变量x变化而变化的规律进行了探究.下面是小刚的探究过程,请将它补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到y1和y2与x的几组对应值:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 4.00 | 3.96 | m | 3.61 | 3.27 | 2.77 | 2.00 |
y2/cm | 0.00 | 0.99 | 1.89 | 2.60 | 2.98 | 2.77 | 0.00 |
经测量,m的值是 ;(保留一位小数)
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),点(x,y2),并画出函数y1, y2的图象;

(3)结合函数图象,回答问题:△APC为等腰三角形时,AP的长度约为 cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com