
【题目】如图,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连接AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.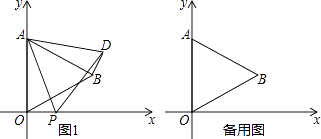
(1)求B的坐标;
(2)当点P运动到点(t,0)时,试用含t的式子表示点D的坐标;
(3)是否存在点P,使△OPD的面积等于 ![]() ,若存在,请求出符合条件的点P的坐标(直接写出结果即可)
,若存在,请求出符合条件的点P的坐标(直接写出结果即可)
【答案】
(1)
解:如图1,

过点B作BE⊥y轴于点E,作BF⊥x轴于点F.
由已知得:BF=OE=2,
∴OF= ![]() =2
=2 ![]() ,
,
∴点B的坐标是(2 ![]() ,2).
,2).
设直线AB的解析式是y=kx+b(k≠0),
则有 ![]() ,
,
∴  .
.
∴直线AB的解析式是y=﹣ ![]() x+4,
x+4,
(2)
解:∵△ABD由△AOP旋转得到,
∴△ABD≌△AOP.
∴AP=AD,∠DAB=∠PAO.
∴∠DAP=∠BAO=60°.
∴△ADP是等边三角形.
如图2,

过点D作DH⊥x轴于点H,延长EB交DH于点G,则BG⊥DH.
在Rt△BDG中,∠BGD=90°,∠DBG=60°,
∴BG=BDcos60°=t× ![]() =
= ![]() .DG=BDsin60°=
.DG=BDsin60°= ![]() t.
t.
∴OH=EG=2 ![]() +
+ ![]() t,DH=2+
t,DH=2+ ![]() t.
t.
∴点D的坐标为(2 ![]() +
+ ![]() t,2+
t,2+ ![]() t).
t).
(3)
解:存在.
假设存在点P,在它的运动过程中,使△OPD的面积等于 ![]() .
.
设点P为(t,0),下面分三种情况讨论:
①当t>0时,如答图2,BD=OP=t,DG= ![]() t,
t,
∴DH=2+ ![]() t.
t.
∵△OPD的面积等于 ![]() ,
,
∴ ![]() t(2+
t(2+ ![]() t)=
t)= ![]() ,
,
∴t1= ![]() ,t2=
,t2= ![]() (舍去).
(舍去).
∴点P1的坐标为( ![]() ,0).
,0).
②∵当D在x轴上时,如图3,

根据锐角三角函数求出BD=OP= ![]() ,
,
∴当﹣ ![]() <t≤0时,如答图1,BD=OP=﹣t,DG=﹣
<t≤0时,如答图1,BD=OP=﹣t,DG=﹣ ![]() t,
t,
∴GH=BF=2﹣(﹣ ![]() t)=2+
t)=2+ ![]() t.
t.
∵△OPD的面积等于 ![]() ,
,
∴﹣ ![]() t(2﹣
t(2﹣ ![]() t)=
t)= ![]() ,
,
∴t1=﹣ ![]() ,t2=﹣
,t2=﹣ ![]()
∴点P2的坐标为(﹣ ![]() ,0),点P3的坐标为(﹣
,0),点P3的坐标为(﹣ ![]() ,0).
,0).
③当t≤﹣ ![]() 时,BD=OP=﹣t,DG=﹣
时,BD=OP=﹣t,DG=﹣ ![]() t,
t,
∴DH=﹣ ![]() t﹣2.
t﹣2.
∵△OPD的面积等于 ![]() ,
,
∴ ![]() (﹣t)(﹣2﹣
(﹣t)(﹣2﹣ ![]() t)=
t)= ![]() ,
,
∴t1= ![]() ,t2=
,t2= ![]() (舍去).
(舍去).
∴点P4的坐标为( ![]() ,0).
,0).
综上所述,点P的坐标分别为P1( ![]() ,0),P2(﹣
,0),P2(﹣ ![]() ,0),P3(﹣
,0),P3(﹣ ![]() ,0),P4(
,0),P4( ![]() ,0).
,0).
【解析】(1)过点B作BE⊥y轴于点E,作BF⊥x轴于点F.依题意得BF=OE=2,利用勾股定理求出OF,然后可得点B的坐标.设直线AB的解析式是y=kx+b,把已知坐标代入可求解.(2)由△ABD由△AOP旋转得到,△ABD≌△AOP,AP=AD,∠DAB=∠PAO,∠DAP=∠BAO=60°,△ADP是等边三角形,利用勾股定理求出DP.在Rt△BDG中,∠BGD=90°,∠DBG=60°.利用三角函数求出BG=BDcos60°,DG=BDsin60°.然后求出OH,DH,然后求出点D的坐标.(3)分三种情况进行讨论:①当P在x轴正半轴上时,即t>0时;②当P在x轴负半轴,但D在x轴上方时;即﹣ ![]() <t≤0时③当P在x轴负半轴,D在x轴下方时,即t≤﹣
<t≤0时③当P在x轴负半轴,D在x轴下方时,即t≤﹣ ![]() 时.综合上面三种情况即可求出符合条件的t的值.
时.综合上面三种情况即可求出符合条件的t的值.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.
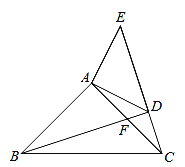
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对x,y定义一种新运算T,规定: ![]() (其中a,b均为非零常数),这里等式右边是通常的四则运算,例如:
(其中a,b均为非零常数),这里等式右边是通常的四则运算,例如: ![]() ,已知T(1,﹣1)=﹣2,T(4,2)=1
,已知T(1,﹣1)=﹣2,T(4,2)=1
(1)求a,b的值;
(2)若关于m的不等式组 ![]() 恰好有4个整数解,求实数p的取值范围.
恰好有4个整数解,求实数p的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】你认为月球上有水吗?如图是对某中学八年级的140名男生的调查结果.

(1)认为“有水”的频数为________,认为“没有水”的频数是_______,认为“不知道”的频数是_______;
(2)认为“有水”的频率为_______,认为“没有水”的频率是______,认为“不知道”的频率是_______,频率之和为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=14,BC=8,点E为边BC上一点,且BE=5,将纸片沿过点E的一条直线l翻折,使点B落在直线CD上,若l与矩形的边的另一个交点为F,则EF的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
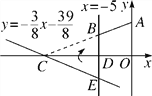
【题目】如图,在平面直角坐标系xOy中,A(0,5),直线x=-5与x轴交于点D,直线y=-![]() x-
x-![]() 与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.
与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.
(1)求点C,E的坐标及直线AB的解析式;
(2)若S=S△CDE+S四边形ABDO,求S的值;
(3)在求(2)中S时,嘉琪有个想法:“将△CDE沿x轴翻折到△CDB的位置,而△CDB与四边形ABDO拼接后可看成△AOC,这样求S便转化为直接求△AOC的面积,如此不更快捷吗?”但大家经反复验算,发现S△AOC≠S,请通过计算解释他的想法错在哪里.
查看答案和解析>>
科目:初中数学 来源: 题型:
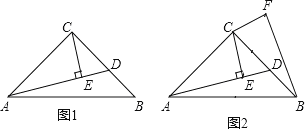
【题目】在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D是边BC上任意一点,连接AD,过点C作CE⊥AD于点E.
(1)如图1,若∠BAD=15°,且CE=1,求线段BD的长;
(2)如图2,过点C作CF⊥CE,且CF=CE,连接BF,
求证:AE=BF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com