
【题目】如图,在矩形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,将
,将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 落在点
落在点![]() 处,且
处,且![]() ,连接
,连接![]() .求证:
.求证:
(![]() )
)![]() 是等边三角形.
是等边三角形.
(![]() )
)![]() .
.
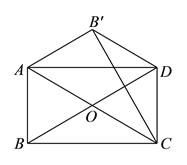
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由四边形ABCD是矩形,得到∠BAD=90°,AO=OD,得到∠OAD=∠ADO,根据平行线的性质得到∠B′AD=∠ADB,等量代换得到∠B′AD=∠DAC,根据折叠的性质得到∠BAC=∠CAB′,得到∠DAC=![]() ∠BAC,求得∠BAC=60°,于是得到结论;(2)连接B′O,推出B′C垂直平分OD,得到B′O=B′D,根据等腰三角形的性质得到∠OB′C=∠OCB′=30°,求得∠OCB′=∠CB′D,于是得到结论.
∠BAC,求得∠BAC=60°,于是得到结论;(2)连接B′O,推出B′C垂直平分OD,得到B′O=B′D,根据等腰三角形的性质得到∠OB′C=∠OCB′=30°,求得∠OCB′=∠CB′D,于是得到结论.
试题解析:( ![]() )∵四边形
)∵四边形![]() 是矩形,
是矩形,
∴![]() ,
, ![]() ,
, ![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() 是由
是由![]() 沿直线
沿直线![]() 翻折得到,
翻折得到,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]() 是等边三角形.
是等边三角形.
(![]() )∵
)∵![]() 是由
是由![]() 沿直线
沿直线![]() 翻折得到,
翻折得到,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
又![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() .
.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两地相距135千米,大小两辆汽车从甲地开往乙地,大汽车比小汽车早出发4小时,小汽车比大汽车早到30分钟,小汽车和大汽车的速度之比为5∶2,求两车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三(1)班要从甲、乙、丙、丁这![]() 名同学中随机选取
名同学中随机选取![]() 名同学参加学校毕业生代表座谈会.求下列事件的概率:
名同学参加学校毕业生代表座谈会.求下列事件的概率:
(![]() )已确定甲参加,另外
)已确定甲参加,另外![]() 人恰好选中乙;
人恰好选中乙;
(![]() )随机选取
)随机选取![]() 名同学,恰好选中甲和乙.
名同学,恰好选中甲和乙.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小敏进行赛跑训练,他们选择了一个土坡,按同一路线同时出发,从坡脚跑到坡顶再原路返回坡脚.他们俩上坡的平均速度不同,下坡的平均速度则是各自上坡平均速度的![]() 倍.设两人出发
倍.设两人出发![]() 后距出发点的距离为ym.图中折线段
后距出发点的距离为ym.图中折线段![]() 表示小明在整个训练中y与x的函数关系.
表示小明在整个训练中y与x的函数关系.
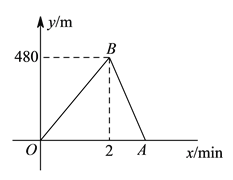
(![]() )点
)点![]() 所表示的实际意义是__________.
所表示的实际意义是__________.
(![]() )求
)求![]() 所在直线的函数表达式.
所在直线的函数表达式.
(![]() )如果小敏上坡平均速度是小明上坡平均速度的一半,那么两人出发后多长时间第一次相遇?
)如果小敏上坡平均速度是小明上坡平均速度的一半,那么两人出发后多长时间第一次相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com