
【题目】如图,抛物线y=ax2+bx+c经过A(﹣3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
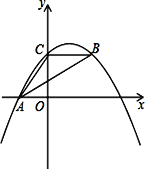
(1)求抛物线的解析式a,b,c;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在求出点M坐标;如果不存在,说明理由.
【答案】(1)抛物线的解析式为y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)线段PQ的最大值为![]() ;
;
(3)符合要求的点M的坐标为(![]() ,9)和(
,9)和(![]() ,﹣11).
,﹣11).
【解析】试题分析:(1)如图1,易证BC=AC,从而得到点B的坐标,然后运用待定系数法求出二次函数的解析式;
(2)如图2,运用待定系数法求出直线AB的解析式.设点P的横坐标为t,从而可以用t的代数式表示出PQ的长,然后利用二次函数的最值性质就可解决问题;
(3)由于AB为直角边,分别以∠BAM=90°(如图3)和∠ABM=90°(如图4)进行讨论,通过三角形相似建立等量关系,就可以求出点M的坐标.
试题解析:(1)如图1,
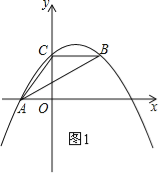
∵A(﹣3,0),C(0,4),
∴OA=3,OC=4.
∵∠AOC=90°,
∴AC=5.
∵BC∥AO,AB平分∠CAO,
∴∠CBA=∠BAO=∠CAB.
∴BC=AC.
∴BC=5.
∵BC∥AO,BC=5,OC=4,
∴点B的坐标为(5,4).
∵A(﹣3.0)、C(0,4)、B(5,4)在抛物线y=ax2+bx+c上,
∴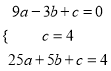
解得: 
∴抛物线的解析式为y=﹣![]() x2+
x2+![]() x+4;
x+4;
(2)如图2,
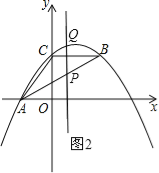
设直线AB的解析式为y=mx+n,
∵A(﹣3.0)、B(5,4)在直线AB上,
∴![]()
解得: ![]()
∴直线AB的解析式为y=![]() x+
x+![]() .
.
设点P的横坐标为t(﹣3≤t≤5),则点Q的横坐标也为t.
∴yP=![]() t+
t+![]() ,yQ=﹣
,yQ=﹣![]() t2+
t2+![]() t+4.
t+4.
∴PQ=yQ﹣yP=﹣![]() t2+
t2+![]() t+4﹣(
t+4﹣(![]() t+
t+![]() )
)
=﹣![]() t2+
t2+![]() t+4﹣
t+4﹣![]() t﹣
t﹣![]()
=﹣![]() t2+
t2+![]() +
+![]()
=﹣![]() (t2﹣2t﹣15)
(t2﹣2t﹣15)
=﹣![]() [(t﹣1)2﹣16]
[(t﹣1)2﹣16]
=﹣![]() (t﹣1)2+
(t﹣1)2+![]() .
.
∵﹣![]() <0,﹣3≤1≤5,
<0,﹣3≤1≤5,
∴当t=1时,PQ取到最大值,最大值为![]() .
.
∴线段PQ的最大值为![]() ;
;
(3)①当∠BAM=90°时,如图3所示.
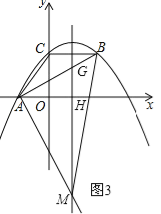
抛物线的对称轴为x=﹣![]() =﹣
=﹣ =
=![]() .
.
∴xH=xG=xM=![]() .
.
∴yG=![]() ×
×![]() +
+![]() =
=![]() .
.
∴GH=![]() .
.
∵∠GHA=∠GAM=90°,
∴∠MAH=90°﹣∠GAH=∠AGM.
∵∠AHG=∠MHA=90°,∠MAH=∠AGM,
∴△AHG∽△MHA.
∴![]() .
.
∴ .
.
解得:MH=11.
∴点M的坐标为(![]() ,﹣11).
,﹣11).
②当∠ABM=90°时,如图4所示.
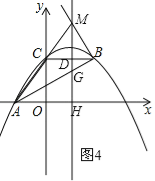
∵∠BDG=90°,BD=5﹣![]() =
=![]() ,DG=4﹣
,DG=4﹣![]() =
=![]() ,
,
∴BG= .
.
同理:AG=![]() .
.
∵∠AGH=∠MGB,∠AHG=∠MBG=90°,
∴△AGH∽△MGB.
∴![]() .
.
∴ .
.
解得:MG=![]() .
.
∴MH=MG+GH=![]() +
+![]() =9.
=9.
∴点M的坐标为(![]() ,9).
,9).
综上所述:符合要求的点M的坐标为(![]() ,9)和(
,9)和(![]() ,﹣11).
,﹣11).


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,OC是∠AOD的平分线,OE是∠BOD的平分线.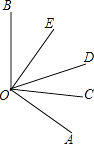
(1)若∠AOB=120°,则∠COE是多少度?
(2)若∠EOC=65°,∠DOC=25°,则∠BOE是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:如图1,圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上.圆心在P(a,b),半径为r的圆的方程可以写为:(x-a)2+(y-b)2=r2.如:圆心在P(2,-1),半径为5的圆的方程为:(x-2)2+(y+1)2=25.
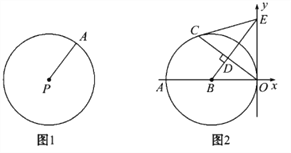
(1)填空: ①以A(3,0)为圆心,1为半径的圆的方程为:________; ②以B(-1,-2)为圆心, ![]() 为半径的圆的方程为:________;
为半径的圆的方程为:________;
(2)根据以上材料解决以下问题:
如图2,以B(-6,0)为圆心的圆与y轴相切于原点,C是☉B上一点,连接OC,作BD⊥OC垂足为D,延长BD交y轴于点E,已知sin∠AOC=![]() .
.
①连接EC,证明EC是☉B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO,若存在,求P点坐标,并写出以P为圆心,以PB为半径的☉P的方程;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中秋佳节我国有赏月和吃月饼的传统,英才学校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了60名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图.(注:参与问卷调查的每一位同学在任何一种分类统计中只有一种选择)请根据统计图完成下列问题:
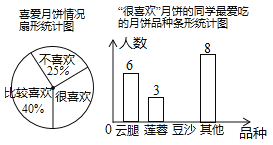
(1)扇形统计图中,“很喜欢”的部分所对应的圆心角为 度;条形统计图中,“很喜欢”月饼中喜欢“豆沙”月饼的学生有 人;
(2)若该校共有学生1200人,请根据上述调查结果,估计该校学生中“很喜欢”月饼的有 人.
(3)李民同学最爱吃莲蓉月饼,陈丽同学最爱吃豆沙月饼,现有重量、包装完全一样的豆沙、莲蓉、蛋黄
三种月饼各一个,让李民、陈丽每人各选一个,则李民、陈丽两人都选中自己最爱吃的月饼的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△OAB中,OA=OB=10,∠AOB=80°,以点O为圆心,6为半径的优弧![]() 分别交OA、OB于点M、N.
分别交OA、OB于点M、N.
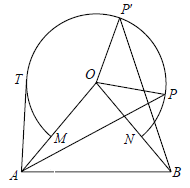
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得OP′. 求证:AP = BP′;
(2)点T在左半弧上,若AT与弧![]() 相切于点T,求点T到OA的距离;
相切于点T,求点T到OA的距离;
(3)设点Q在优弧![]() 上,当△AOQ的面积最大时,直接写出∠BOQ的度数.
上,当△AOQ的面积最大时,直接写出∠BOQ的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com