
،¾جâؤ؟،؟خھءث¸ü؛أضخہيؤ³؛ث®ضت£¬±£»¤»·¾³£¬تذضخخغ¹«ث¾¾ِ¶¨¹؛آٍ![]() ج¨خغث®´¦ہية豸£®دضسذ
ج¨خغث®´¦ہية豸£®دضسذ![]() £¬
£¬![]() ء½ضضذح؛إµؤة豸£¬ئنضذأ؟ج¨µؤ¼غ¸ٌ£¬شآ´¦ہيخغث®ء؟بçدآ±ي£®¾µ÷²é£؛¹؛آٍز»ج¨
ء½ضضذح؛إµؤة豸£¬ئنضذأ؟ج¨µؤ¼غ¸ٌ£¬شآ´¦ہيخغث®ء؟بçدآ±ي£®¾µ÷²é£؛¹؛آٍز»ج¨![]() ذحة豸±ب¹؛آٍز»ج¨
ذحة豸±ب¹؛آٍز»ج¨![]() ذحة豸¶à
ذحة豸¶à![]() حٍشھ£¬¹؛آٍ
حٍشھ£¬¹؛آٍ![]() ج¨
ج¨![]() ذحة豸±ب¹؛آٍ
ذحة豸±ب¹؛آٍ![]() ج¨
ج¨![]() ذحة豸ةظ
ذحة豸ةظ![]() حٍشھ£®
حٍشھ£®
|
| |
¼غ¸ٌ£¨حٍشھ/ج¨£© |
|
|
´¦ہيخغث®ء؟£¨¶ض/شآ£© |
|
|
£¨![]() £©اَ
£©اَ![]() £¬
£¬![]() µؤضµ£®
µؤضµ£®
£¨![]() £©¾ش¤ثم£؛تذضخخغ¹«ث¾¹؛آٍخغث®´¦ہية豸µؤ×ت½ً²»³¬¹
£©¾ش¤ثم£؛تذضخخغ¹«ث¾¹؛آٍخغث®´¦ہية豸µؤ×ت½ً²»³¬¹![]() حٍشھ£¬ؤمبدخھ¸أ¹«ث¾سذؤؤ¼¸ضض¹؛آٍ·½°¸£®
حٍشھ£¬ؤمبدخھ¸أ¹«ث¾سذؤؤ¼¸ضض¹؛آٍ·½°¸£®
£¨![]() £©شع£¨
£©شع£¨![]() £©ختµؤجُ¼دآ£¬بôأ؟شآزھاَ´¦ہي¸أ؛µؤخغث®ء؟²»µحسع
£©ختµؤجُ¼دآ£¬بôأ؟شآزھاَ´¦ہي¸أ؛µؤخغث®ء؟²»µحسع![]() ¶ض£¬خھءث½عش¼×ت½ً£¬اëؤمخھضخخغ¹«ث¾ةè¼ئز»ضض×îت،ا®µؤ¹؛آٍ·½°¸£®
¶ض£¬خھءث½عش¼×ت½ً£¬اëؤمخھضخخغ¹«ث¾ةè¼ئز»ضض×îت،ا®µؤ¹؛آٍ·½°¸£®
،¾´ً°¸،؟(1)a=12,b=10;£¨ 2£©¼û½âخِ,£¨ 3£©س¦ر،¹؛ Aذحة豸1 ج¨£¬ Bذحة豸9 ج¨
،¾½âخِ،؟تشجâ·ضخِ£؛£¨1£©زٍخھ¹؛آٍز»ج¨Aذحة豸±ب¹؛آٍز»ج¨Bذحة豸¶à2حٍشھ£¬¹؛آٍ2ج¨Aذحة豸±ب¹؛آٍ3ج¨Bذحة豸ةظ6حٍشھ£¬ثùزشسذ![]() £¬½âض®¼´؟ة£»
£¬½âض®¼´؟ة£»
£¨2£©؟ةةè¹؛آٍخغث®´¦ہية豸Aذحة豸xج¨£¬Bذحة豸![]() ج¨£¬شٍسذ
ج¨£¬شٍسذ![]() £¬½âض®ب·¶¨xµؤضµ£¬¼´؟ةب·¶¨·½°¸£»
£¬½âض®ب·¶¨xµؤضµ£¬¼´؟ةب·¶¨·½°¸£»
£¨3£©أ؟شآزھاَ´¦ہيرَہ½؛µؤخغث®ء؟²»µحسع1860¶ض£¬سذ![]() £¬½âض®¼´؟ةسةxµؤضµب·¶¨·½°¸£¬ب»؛َ½ّذذ±ب½د£¬×÷³ِر،شٌ£®
£¬½âض®¼´؟ةسةxµؤضµب·¶¨·½°¸£¬ب»؛َ½ّذذ±ب½د£¬×÷³ِر،شٌ£®
تشجâ½âخِ£؛£¨![]() £©سةجâزâµأ
£©سةجâزâµأ![]() £¬
£¬
½âµأ![]() £®
£®
£¨![]() £©ةè¹؛آٍ
£©ةè¹؛آٍ![]() ذحة豸
ذحة豸![]() ج¨£¬
ج¨£¬![]() ذحة豸
ذحة豸![]() ج¨£¬
ج¨£¬
![]() £¬
£¬
½âµأ![]() £¬
£¬
،ك![]() ب،·ا¸؛صûت£¬
ب،·ا¸؛صûت£¬
،à![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬
،à![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬
،àسذبضض¹؛آٍ·½°¸£؛
¢ظ![]() ذحة豸
ذحة豸![]() ج¨£¬
ج¨£¬![]() ذحة豸
ذحة豸![]() ج¨£®
ج¨£®
¢ع![]() ذحة豸
ذحة豸![]() ج¨£¬
ج¨£¬![]() ذحة豸
ذحة豸![]() ج¨£®
ج¨£®
¢غ![]() ذحة豸
ذحة豸![]() ج¨£¬
ج¨£¬![]() ذحة豸
ذحة豸![]() ج¨£®
ج¨£®
£¨![]() £©سةجâزâµأ£¬
£©سةجâزâµأ£¬![]() £¬
£¬
،à![]() £¬
£¬
،ك![]() £¬
£¬
،à![]() £¬
£¬![]() £®
£®
µ±![]() ت±£¬¹؛آٍ×ت½ًخھ
ت±£¬¹؛آٍ×ت½ًخھ![]() £¨حٍشھ£©£¬
£¨حٍشھ£©£¬
µ±![]() ت±£¬¹؛آٍ×ت½ًخھ
ت±£¬¹؛آٍ×ت½ًخھ![]() £¨حٍشھ£©£¬
£¨حٍشھ£©£¬
،àخھءث½عش¼×ت½ً£¬س¦ر،¹؛![]() ذحة豸
ذحة豸![]() ج¨£¬
ج¨£¬![]() ذحة豸
ذحة豸![]() ج¨£®
ج¨£®



| ؤ꼶 | ¸كضذ؟خ³ج | ؤ꼶 | ³ُضذ؟خ³ج |
| ¸كز» | ¸كز»أâ·ر؟خ³جحئ¼ِ£، | ³ُز» | ³ُز»أâ·ر؟خ³جحئ¼ِ£، |
| ¸ك¶ | ¸ك¶أâ·ر؟خ³جحئ¼ِ£، | ³ُ¶ | ³ُ¶أâ·ر؟خ³جحئ¼ِ£، |
| ¸كب | ¸كبأâ·ر؟خ³جحئ¼ِ£، | ³ُب | ³ُبأâ·ر؟خ³جحئ¼ِ£، |
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟خھءث´«³ذسإذم´«ح³خؤ»¯£¬ؤ³ذ£؟ھص¹،°¾µنثذ¶ء،±±ببü»î¶¯£¬ثذ¶ء²ؤءدسذ،¶آغسï،·£¬،¶ب×ض¾،·£¬،¶µـ×س¹و،·£¨·ض±ًسأ×ضؤ¸A£¬B£¬Cزہ´خ±يت¾صâب¸ِثذ¶ء²ؤءد£©£¬½«A£¬B£¬Cصâب¸ِ×ضؤ¸·ض±ًذ´شع3صإحêب«دàح¬µؤ²»ح¸أ÷؟¨ئ¬µؤصأوةد£¬°رصâ3صإ؟¨ئ¬±³أو³¯ةدد´شب؛َ·إشع×ہأوةد£®ذ،أ÷؛حذ،ءء²خ¼سثذ¶ء±ببü£¬±ببüت±ذ،أ÷دب´سضذثو»ْ³éب،ز»صإ؟¨ئ¬£¬¼اآ¼دآ؟¨ئ¬ةدµؤؤعبف£¬·إ»ط؛َد´شب£¬شظسةذ،ءء´سضذثو»ْ³éب،ز»صإ؟¨ئ¬£¬ر،تض°´¸÷×ش³éب،µؤ؟¨ئ¬ةدµؤؤعبف½ّذذثذ¶ء±ببü£®
£¨1£©ذ،أ÷ثذ¶ء،¶آغسï،·µؤ¸إآتتا،، ،،.
£¨2£©اëسأءذ±ي·¨»ٍ»ت÷×´ح¼·¨اَذ،أ÷؛حذ،ءءثذ¶ءء½¸ِ²»ح¬²ؤءدµؤ¸إآت£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟دآءذشثثمسذ´يخَµؤتا£¨،،،،£©
A. ©پ5+£¨+3£©£½8B. 5©پ£¨©پ2£©£½7C. ©پ9،ء£¨©پ3£©£½27D. ©پ4،ء£¨©پ5£©£½20
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟زرضھض±دكm،خn£¬µمCتاض±دكmةدز»µم£¬µمDتاض±دكnةدز»µم£¬CDسëض±دكm،¢n²»´¹ض±£¬µمPخھدك¶خCDµؤضذµم£®
£¨1£©²ظ×÷·¢دض£؛ض±دكl،حm£¬l،حn£¬´¹×م·ض±ًخھA،¢B£¬µ±µمAسëµمCضط؛دت±£¨بçح¼¢ظثùت¾£©£¬ء¬½سPB£¬اëض±½سذ´³ِدك¶خPAسëPBµؤتء؟¹طدµ£؛،، ،،£®
£¨2£©²آدëض¤أ÷£؛شعح¼¢ظµؤاé؟ِدآ£¬°رض±دكlدٍةدئ½زئµ½بçح¼¢عµؤخ»ضأ£¬تشخت£¨1£©ضذµؤPAسëPBµؤ¹طدµت½تا·ٌبشب»³ةء¢£؟بô³ةء¢£¬اëض¤أ÷£»بô²»³ةء¢£¬اëثµأ÷ہيسة£®
£¨3£©رسةىج½¾؟£؛شعح¼¢عµؤاé؟ِدآ£¬°رض±دكlبئµمAذ×ھ£¬ت¹µأ،دAPB=90،م£¨بçح¼¢غثùت¾£©£¬بôء½ئ½ذذدكm،¢nض®¼نµؤ¾àہëخھ2k£®اَض¤£؛PAPB=kAB£®

²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
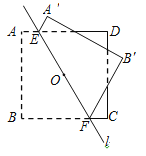
،¾جâؤ؟،؟بçح¼£¬ص·½ذخABCDµؤ±ك³¤خھ2£¬µمOتاص·½ذخµؤضذذؤ£¬¹µمO×÷ز»جُض±دكl·ض±ً½»ص·½ذخAD£¬BCء½±كسعµمE£¬F.ض±دكl½«ص·½ذخ·ض³ةء½²؟·ض£¬½«ئنضذµؤز»¸ِ²؟·ضرطصâجُض±دك·صغµ½ءيز»¸ِ²؟·ضةد£¬بôAE£½![]() £¬شٍء½¸ِ²؟·ضح¼ذخضذ²»ضطµ²؟·ضµؤأو»خھ_______£®
£¬شٍء½¸ِ²؟·ضح¼ذخضذ²»ضطµ²؟·ضµؤأو»خھ_______£®
²é؟´´ً°¸؛ح½âخِ>>
؟ئؤ؟£؛³ُضذتر§ ہ´ش´£؛ جâذح£؛
،¾جâؤ؟،؟ہûأٌضض×سإàس»ùµطسأA،¢B،¢Cبضضذح؛إµؤسٌأ×ضض×س¹²1500ء£½ّذذ·¢ر؟تشر飬´سضذر،³ِ·¢ر؟آت¸كµؤضض×س½ّذذحئ¹م£®ح¨¹تشرéضھµہ£¬Cذح؛إضض×سµؤ·¢ر؟آتخھ80%£¬¸ù¾فتشرéت¾ف»وضئءثدآأوء½¸ِ²»حêصûµؤح³¼ئح¼(ح¼1،¢ح¼2)£؛
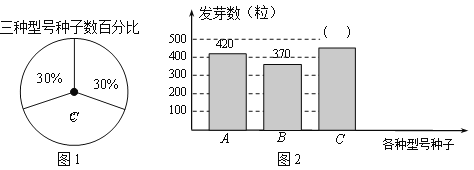
£¨1£©Cذح؛إضض×سµؤ·¢ر؟تتا_________ء££»
£¨2£©ض±½سذ´³ِس¦ر،ؤؤضضذح؛إµؤضض×س½ّذذحئ¹م£؟
£¨3£©بç¹û½«ثùسذزر·¢ر؟µؤضض×س·إµ½ز»ئً£¬´سضذثو»ْب،³ِز»ء££¬اَب،µ½Cذح؛إ·¢ر؟ضض×سµؤ¸إآت£®
²é؟´´ً°¸؛ح½âخِ>>
¹ْ¼تر§ذ£سإر، - ء·د°²لءذ±ي - تشجâءذ±ي
؛±±ت،»¥ءھحّخ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨ئ½ج¨ | حّةدسذ؛¦ذإد¢¾ظ±¨×¨اّ | µçذإص©ئ¾ظ±¨×¨اّ | ةوہْت·ذéخقض÷زهسذ؛¦ذإد¢¾ظ±¨×¨اّ | ةوئَاضب¨¾ظ±¨×¨اّ
خ¥·¨؛ح²»ء¼ذإد¢¾ظ±¨µç»°£؛027-86699610 ¾ظ±¨ستدن£؛58377363@163.com