
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() .点
.点![]() 为
为![]() 轴上一动点,过点
轴上一动点,过点![]() 且垂直于
且垂直于![]() 轴的直线分别交直线
轴的直线分别交直线![]() 及抛物线于点
及抛物线于点![]() ,
,![]() .
.
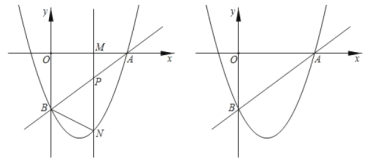
(1)填空:点![]() 的坐标为_________,抛物线的解析式为_________;
的坐标为_________,抛物线的解析式为_________;
(2)当点![]() 在线段
在线段![]() 上运动时(不与点
上运动时(不与点![]() ,
,![]() 重合),
重合),
①当![]() 为何值时,线段
为何值时,线段![]() 最大值,并求出
最大值,并求出![]() 的最大值;
的最大值;
②求出使![]() 为直角三角形时
为直角三角形时![]() 的值;
的值;
(3)若抛物线上有且只有三个点![]() 到直线
到直线![]() 的距离是
的距离是![]() ,请直接写出此时由点
,请直接写出此时由点![]() ,
,![]() ,
,![]() ,
,![]() 构成的四边形的面积.
构成的四边形的面积.
【答案】(1)![]() ,
,![]() ;
;
(2)①当![]() 时,
时,![]() 有最大值是3; ②使
有最大值是3; ②使![]() 为直角三角形时
为直角三角形时![]() 的值为3或
的值为3或![]() ;
;
(3)点![]() ,
,![]() ,
,![]() ,
,![]() 构成的四边形的面积为:6或
构成的四边形的面积为:6或![]() 或
或![]() .
.
【解析】
(1)把点A坐标代入直线表达式y=![]() ,求出a=3,把点A、B的坐标代入二次函数表达式,即可求解;
,求出a=3,把点A、B的坐标代入二次函数表达式,即可求解;
(2)①设:点P(m,![]() ),N(m,
),N(m,![]() )求出PN值的表达式,即可求解;②分∠BNP=90°、∠NBP=90°、∠BPN=90°三种情况,求解即可;
)求出PN值的表达式,即可求解;②分∠BNP=90°、∠NBP=90°、∠BPN=90°三种情况,求解即可;
(3)若抛物线上有且只有三个点N到直线AB的距离是h,则只能出现:在AB直线下方抛物线与过点N的直线与抛物线有一个交点N,在直线AB上方的交点有两个,分别求解即可.
解:(1)把点![]() 坐标代入直线表达式
坐标代入直线表达式![]() ,
,
解得:![]() ,则:直线表达式为:
,则:直线表达式为:![]() ,令
,令![]() ,则:
,则:![]() ,
,
则点![]() 坐标为
坐标为![]() ,
,
将点![]() 的坐标代入二次函数表达式得:
的坐标代入二次函数表达式得:![]() ,
,
把点![]() 的坐标代入二次函数表达式得:
的坐标代入二次函数表达式得:![]() ,
,
解得:![]() ,
,
故:抛物线的解析式为:![]() ,
,
故:答案为:![]() ,
,![]() ;
;
(2)①∵![]() 在线段
在线段![]() 上,且
上,且![]() 轴,
轴,
∴点![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴抛物线开口向下,
∴当![]() 时,
时,![]() 有最大值是3,
有最大值是3,
②当![]() 时,点
时,点![]() 的纵坐标为-3,
的纵坐标为-3,
把![]() 代入抛物线的表达式得:
代入抛物线的表达式得:![]() ,解得:
,解得:![]() 或0(舍去
或0(舍去![]() ),
),
∴![]() ;
;
当![]() 时,∵
时,∵![]() ,两直线垂直,其
,两直线垂直,其![]() 值相乘为-1,
值相乘为-1,
设:直线![]() 的表达式为:
的表达式为:![]() ,
,
把点![]() 的坐标代入上式,解得:
的坐标代入上式,解得:![]() ,则:直线
,则:直线![]() 的表达式为:
的表达式为:![]() ,
,
将上式与抛物线的表达式联立并解得:![]() 或0(舍去
或0(舍去![]() ),
),
当![]() 时,不合题意舍去,
时,不合题意舍去,
故:使![]() 为直角三角形时
为直角三角形时![]() 的值为3或
的值为3或![]() ;
;
(3)∵![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,则:
,则:![]() ,
,![]() ,
,
∵![]() 轴,
轴,
∴![]() ,
,
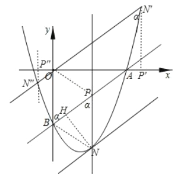
若抛物线上有且只有三个点![]() 到直线
到直线![]() 的距离是
的距离是![]() ,
,
则只能出现:在![]() 直线下方抛物线与过点
直线下方抛物线与过点![]() 的直线与抛物线有一个交点
的直线与抛物线有一个交点![]() ,在直线
,在直线![]() 上方的交点有两个.
上方的交点有两个.
当过点![]() 的直线与抛物线有一个交点
的直线与抛物线有一个交点![]() ,
,
点![]() 的坐标为
的坐标为![]() ,设:点
,设:点![]() 坐标为:
坐标为:![]() ,
,
则:![]() ,过点
,过点![]() 作
作![]() 的平行线,
的平行线,
则点![]() 所在的直线表达式为:
所在的直线表达式为:![]() ,将点
,将点![]() 坐标代入,
坐标代入,
解得:过![]() 点直线表达式为:
点直线表达式为:![]() ,
,
将拋物线的表达式与上式联立并整理得:![]() ,
,
![]() ,
,
将![]() 代入上式并整理得:
代入上式并整理得:![]() ,
,
解得:![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
则:点![]() 坐标为
坐标为![]() ,则:
,则:![]() ,
,
∵![]() ,
,![]() ,∴四边形
,∴四边形![]() 为平行四边形,则点
为平行四边形,则点![]() 到直线
到直线![]() 的距离等于点
的距离等于点![]() 到直线
到直线![]() 的距离,
的距离,
即:过点![]() 与
与![]() 平行的直线与抛物线的交点为另外两个
平行的直线与抛物线的交点为另外两个![]() 点,即:
点,即:![]() 、
、![]() ,
,
直线![]() 的表达式为:
的表达式为:![]() ,将该表达式与二次函数表达式联立并整理得:
,将该表达式与二次函数表达式联立并整理得:
![]() ,解得:
,解得:![]() ,
,
则点![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() ,
,![]() ,
,
作![]() 交直线
交直线![]() 于点
于点![]() ,
,
则![]() ,
,
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,则:
,则:![]() ,
,![]() ,
,
![]() ,
,
则:![]() ,
,
同理:![]() ,
,
故:点![]() ,
,![]() ,
,![]() ,
,![]() 构成的四边形的面积为:6或
构成的四边形的面积为:6或![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
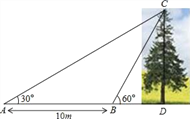
【题目】如图,某数学兴趣小组想测量一棵树CD的高度,他们先在点A处测得树顶C的仰角为30°,然后沿AD方向前行10m,到达B点,在B处测得树顶C的仰角高度为60°(A、B、D三点在同一直线上).请你根据他们测量数据计算这棵树CD的高度(结果精确到0.1m).(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
【答案】8.7米
【解析】试题分析:首先利用三角形的外角的性质求得∠ACB的度数,得到BC的长度,然后在直角△BDC中,利用三角函数即可求解.
试题解析:∵∠CBD=∠A+∠ACB,
∴∠ACB=∠CBD﹣∠A=60°﹣30°=30°,
∴∠A=∠ACB,
∴BC=AB=10(米).
在直角△BCD中,CD=BCsin∠CBD=10×![]() =5
=5![]() ≈5×1.732=8.7(米).
≈5×1.732=8.7(米).
答:这棵树CD的高度为8.7米.
考点:解直角三角形的应用
【题型】解答题
【结束】
23
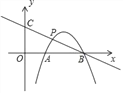
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+ax+b交x轴于A(1,0),B(3,0)两点,点P是抛物线上在第一象限内的一点,直线BP与y轴相交于点C.
(1)求抛物线y=﹣x2+ax+b的解析式;
(2)当点P是线段BC的中点时,求点P的坐标;
(3)在(2)的条件下,求sin∠OCB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
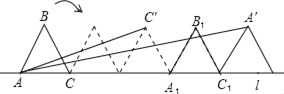
【题目】如图,已知边长为2的正三角形ABC沿着直线l滚动.
(1)当△ABC滚动一周到△A1B1C1的位置,此时A点运动的路程为 ;约为 ;(精确到0.1,π=3.14…)
(2)设△ABC滚动240°时,C点的位置为C′,△ABC滚动480°时,A点的位置为A′.请你利用三角函数中正切的两角和公式tan(α+β)=(tanα+tanβ)÷(1﹣tanαtanβ),求出∠CAC′+∠CAA′的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个二次函数图象的顶点,开口方向都相同,则称这两个二次函数为“同簇二次函数”。
(1)请写出两个为“同簇二次函数”的函数;
(2)已知关于x的二次函数y1=2x2—4mx+2m2+1,和y2=ax2+bx+5,其中y1的图象经过点A(1,1),若y1+y2为y1为“同簇二次函数”,求函数y2的表达式,并求当0≤x≤3时,y2的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面
的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如下图)
你选择的方案是_____(填方案一,方案二,或方案三),则B点坐标是______,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为调查本校学生平均每天完成作业所用时间的情况,随机调查了50名同学,如图是根据调查所得数据绘制的统计图的一部分.
请根据以上信息,解答下列问题:
(1)将统计图补充完整;
(2)若该校共有1 800名学生,根据以上调查结果估计该校全体学生平均每天完成作业所用总时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果点D、E分别在△ABC中的边AB和AC上,那么不能判定DE∥BC的比例式是( )
A. AD:DB=AE:EC B. DE:BC=AD:AB
C. BD:AB=CE:AC D. AB:AC=AD:AE
查看答案和解析>>
科目:初中数学 来源: 题型:
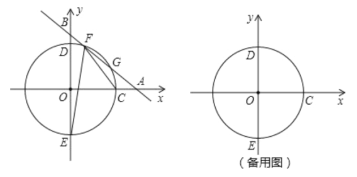
【题目】如图,平面直角坐标系![]() 中,一次函数
中,一次函数![]() (
(![]() 为常数,
为常数,![]() )的图像与
)的图像与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() ,半径为4的⊙
,半径为4的⊙![]() 与
与![]() 轴正半轴相交于点
轴正半轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 在点
在点![]() 上方.
上方.
(1)若直线![]() 与弧
与弧![]() 有两个交点
有两个交点![]() .
.
①求![]() 的度数;
的度数;
②用含![]() 的代数式表示
的代数式表示![]() ,并直接写出
,并直接写出![]() 的取值范围;
的取值范围;
(2)设![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() ?若存在,请求出
?若存在,请求出![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,P是CB边上一动点,连接AP,作PQ⊥AP交AB于Q.已知AC=3cm,BC=6cm,设PC的长度为xcm,BQ的长度为ycm.
小青同学根据学习函数的经验对函数y随自变量x的变化而变化的规律进行了探究.
下面是小青同学的探究过程,请补充完整:
(1)按照下表中自变量x的值进行取点、画图、测量,分别得到了y的几组对应值;
x/cm | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 6 |
y/cm | 0 | 1.56 | 2.24 | 2.51 | m | 2.45 | 2.24 | 1.96 | 1.63 | 1.26 | 0.86 | 0 |
(说明:补全表格时,相关数据保留一位小数)
m的值约为多少cm;
(2)在平面直角坐标系中,描出以补全后的表格中各组数值所对应的点(x,y),画出该函数的图象;

(3)结合画出的函数图象,解决问题:
①当y>2时,写出对应的x的取值范围;
②若点P不与B,C两点重合,是否存在点P,使得BQ=BP?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com